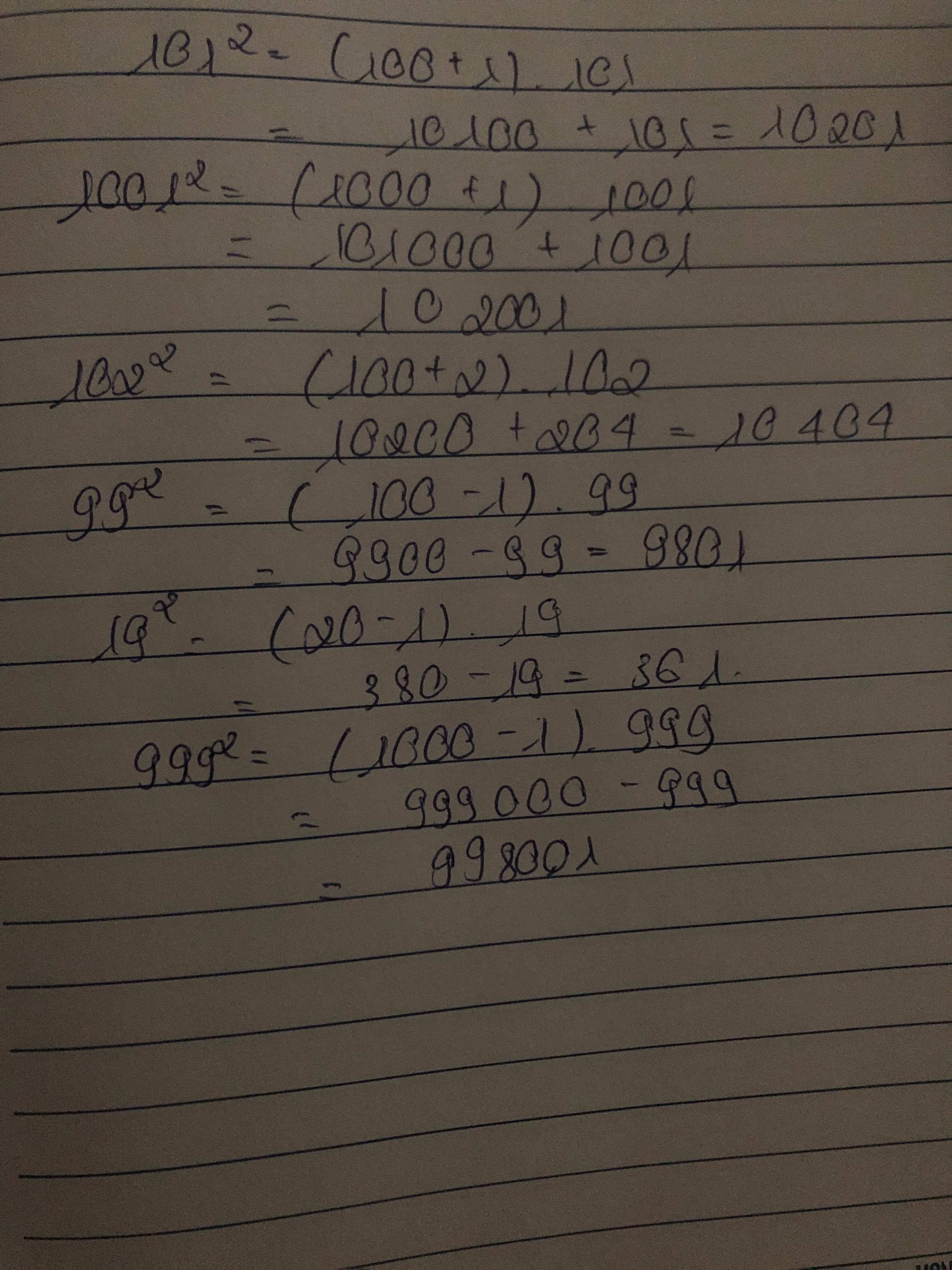chứng minh rằng: 10012+10022+10042-10062=10002+10032+10052-10072
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AK
29 tháng 5 2018
Ta có :
\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{100^2}< \frac{1}{2^2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{99.100}\)
\(\Rightarrow A< \frac{1}{2^2}+\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{99}-\frac{1}{100}\right)\)
\(\Rightarrow A< \frac{1}{4}+\left(\frac{1}{2}-\frac{1}{100}\right)\)
\(\Rightarrow A< \left(\frac{1}{4}+\frac{1}{2}\right)-\frac{1}{100}\)
\(\Rightarrow A< \frac{3}{4}-\frac{1}{100}\)
\(\Rightarrow A< \frac{3}{4}\left(Đpcm\right)\)
~ Ủng hộ nhé
30 tháng 10 2015
1+2+3+4+5.........+10032
=\(\frac{10032.\left(10032+1\right)}{2}\)
=100651056/2
=50325528
28 tháng 7 2021
\(101^2=\left(100+1\right)^2=10000+200+1=10201\)
\(1001^2=\left(1000+1\right)^2=1000000+2000+1=1002001\)
\(102^2=\left(100+2\right)^2=10000+400+4=10404\)
\(99^2=\left(100-1\right)^2=10000-200+1=9801\)
\(19^2=\left(10+9\right)^2=100+180+81=361\)
\(999^2=\left(1000-1\right)^2=1000000-2000+1=998001\)
NT
2
4 tháng 5 2022
A \(=400\) x \(5+7\)
A \(=2000+7\)
A \(=2007\)
Vậy A = 2007
B \(=10042\) x \(5+7\)
B \(=50210+7=20217\)
Vậy B = 20217
B mik không biết là cái đề như A hay là khác tại vì bạn chưa cho đề của B là gì
KC
0
VQ
30 tháng 4 2022
25 : 0,1 = 250
48 : 0,01 = 4800
95 : 0,1 = 950
25 x 10 = 250
48 x 100 = 4800
72 : 0,01 = 7200
b) 11 : 0,25 = 44
32 : 0,5 = 64
75 : 0,5 = 150
11 x 4 = 44
32 x 2 = 64
125 : 0,25 = 500