Cho AB vuông góc với CD và cắt nhau tại trung điểm của mỗi đoạn.
a,CMR:các đoạn AC;CB;BD;DA bằng nhau.
b,tìm tia phân giác của các góc khác góc bẹt trong hình vẽ.Giải thích
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{AOD}=\widehat{BOC}\)
OD=OC
Do đó: ΔOAD=ΔOBC
b: Xét tứ giác ACBD có
O là trung điểm của AB
O là trung điểm của CD
Do đó: ACBD là hình bình hành
Suy ra: BC//AD

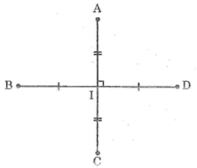
Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm

A C B D M
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.

Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm