Buổi Sinh hoạt CLB Toán - HOC24 team thứ - Lần 3
Chào các bạn nhé :) Vẫn đúng như kế hoạch, hôm nay, thứ Sáu ngày 19/07/2019, bọn mình sẽ đăng một số bài toán để các thành viên team thứ 6 sinh hoạt. Với các câu trả lời đúng và chính xác, các bạn sẽ được cộng điểm giá trị như đã thông báo.
I. Thời gian thi : từ 20h00 đến 21h30 ( 1 tiếng rưỡi ) có thê nạp vaò sau hoac trc 5 phút
II: Bài thi gồm 3 câu co ban; 7 câu nâng cao
Câu 1: Tính nhanh:
\(a,34.34+17.31+17\)
\(b,\frac{1}{3}+\frac{4}{5}-\left(\frac{-1}{5}\right)+\frac{2}{3}-\frac{4}{3}-\frac{2}{3}\)
Câu 2 So Sánh:
\(a,\left(-99\right)^{98}\text{ và }\left(-98\right)^{99}\)
\(b,2^{300}\text{ và: }3^{200}\)
\(c,\frac{9}{10}\text{ và }\frac{11}{12}\)
Câu 3: tìm x
\(a,\left|x-3\right|=x-3\)
\(b,\left|x+5\right|=-5-x\)
Câu 4: Cho: x+y+1=0. Tính:
\(x^3+x^2y+x^2+xy^2+x^2y+xy+2019\)
Câu 5: Cho tam giác cân ABC (AB=AC). Trên cạnh BC lấy điêm D, trên tia đối cua CB lấy điêm E sao cho BD=CE. Các đưong thang vuông góc voi BC ker từ D và E cat AB,AC lần lưọt tại M,N. Chưng minh:
a,DM=EN
b, đưong thang BC cat tại trung điêm I cua MN
Câu 6: Tìm các cap so nguyên tô: a,b,c sao cho:
a2+5ab+b2=7c
Câu 7: Chứng minh:
\(1-\frac{1}{2}+\frac{1}{3}-....+\frac{1}{49}-\frac{1}{50}=\frac{1}{26}+\frac{1}{27}+.....+\frac{1}{50}\)
Câu 8:
Tìm các sô nguyên tô: a1;a2;a3;....;a8
sao cho:a12+a22+.....+a72=a82
Câu 9. Giai phưong trình nghiệm nguyên:
\(x^3+2x=2018-y^2\)
Câu 10. Tìm n sao cho:
n(n+1)(n+2)(n+3)=1680
xin moi a tth tag hộ e


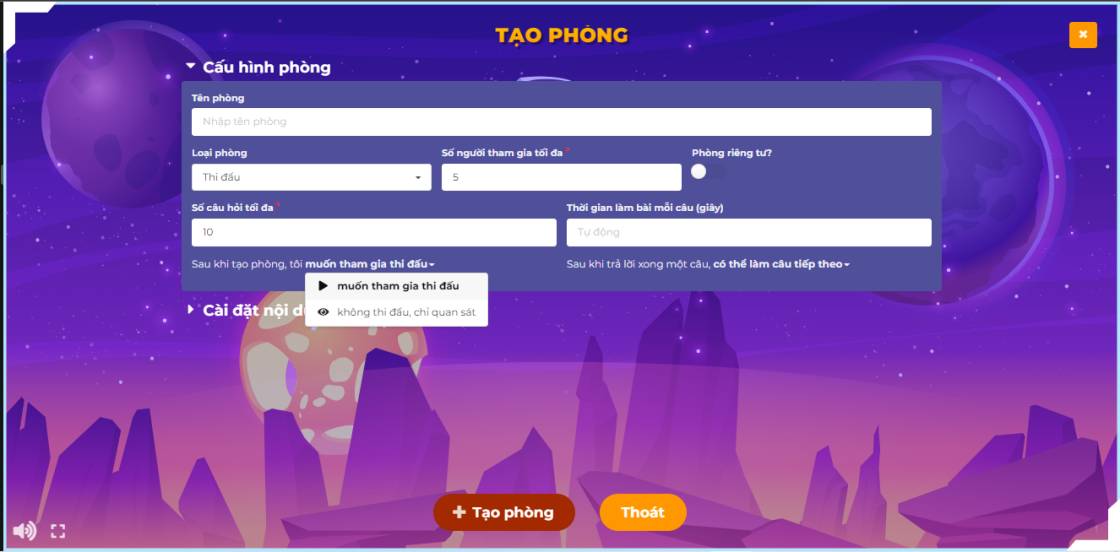 ✔ Không chỉ tạo phòng riêng mà các bạn còn có thể tham gia các phòng do người khác tạo với chủ đề, khối lớp, số lượng người tham gia và liệu phòng thi đã bắt đầu chưa hiện lên trước khi các bạn quyết định nhấn vào phòng thi đấu.
✔ Không chỉ tạo phòng riêng mà các bạn còn có thể tham gia các phòng do người khác tạo với chủ đề, khối lớp, số lượng người tham gia và liệu phòng thi đã bắt đầu chưa hiện lên trước khi các bạn quyết định nhấn vào phòng thi đấu. 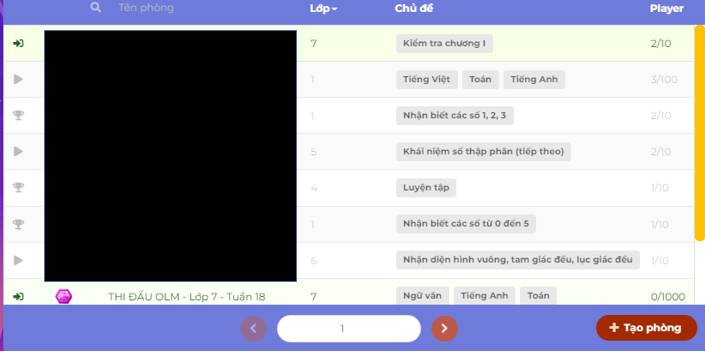
1/ a, \(34.34+17.31+17=17\left(34.2+31+1\right)=17.100=1700\)
b,\(\frac{1}{3}+\frac{4}{5}-\left(\frac{-1}{5}\right)+\frac{2}{3}-\frac{4}{3}-\frac{2}{3}=\left(\frac{1}{3}-\frac{4}{3}\right)+\left(\frac{4}{5}+\frac{1}{5}\right)=\frac{-3}{3}+\frac{5}{5}=-1+1=0\)
2/ a, Vì (-99)98 là số âm có số mũ chẵn nên (-99)98 > 0
(-98)99 là số âm có số mũ lẻ nên (-98)99 < 0
Vậy (-99)98>(-98)99
b, \(2^{300}=\left(2^3\right)^{100}=8^{100};3^{200}=\left(3^2\right)^{100}=9^{100}\)
Vì \(8< 9\Rightarrow8^{100}< 9^{100}\Rightarrow2^{300}< 3^{200}\)
Vậy 2^300 < 3^200
3, a, \(\left|x-3\right|=x-3\)
ĐK: \(x-3\ge0\Leftrightarrow x\ge3\)
Khi đó, \(pt\Leftrightarrow\left[{}\begin{matrix}x-3=x-3\\x-3=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0=0\\x=0\left(ktmdk\right)\end{matrix}\right.\)
Vậy pt đúng với mọi x>=3
b, \(\left|x+5\right|=-5-x\)
ĐK: \(-5-x\ge0\Leftrightarrow x\le-5\)
Khi đó, \(pt\Leftrightarrow\left[{}\begin{matrix}x+5=-5-x\\x+5=x+5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(tm\right)\\0=0\end{matrix}\right.\)
Vậy pt đúng với mọi x<=-5
4,\(x^3+x^2y+x^2+xy^2+x^2y+xy+2019=x^2\left(x+y+1\right)+xy\left(x+y+1\right)+2019=2019 \)
5,
a, Xét t/g BMD và t/g CNE có:
BD=CE (gt)
góc BDM = góc CEN = 90 độ (gt)
góc B = góc C2 (cùng bằng góc C1)
=> t/g BMD = t/g CNE (g.c.g)
=>DM=EN (đpcm)
b, ta có: DM _|_ BC (gt), EN _|_ BC (gt)
=> DM//EN => góc DMI = góc INE (so le trong)
Xét t/g DMI và t/g ENI có:
góc IDM = góc IEN = 90 độ (gt)
DM = EN (cm câu a)
góc DMI = góc INE (cmt)
=> t/g DMI = t/g ENI (g.c.g)
=> MI = NI
Vậy đưong thang BC cat tại trung điêm I cua MN
6, Ta có \(7^c⋮7\Rightarrow a^2+5ab+b^2⋮7\Rightarrow a^2+5ab+b^2-7ab⋮7\)
=> \(a^2-2ab+b^2⋮7\Rightarrow\left(a-b\right)^2⋮7\Rightarrow a-b⋮7\) (vì 7 là số nguyên tố)=>\(\left(a-b\right)^2⋮49\)
Vì c là số nguyên tố => c>1 => \(7^c⋮49\)
=> \(a^2-5ab+b^2-\left(a^2-2ab+b^2\right)⋮49\)
=> \(7ab⋮49\Rightarrow ab⋮7\Rightarrow\left[{}\begin{matrix}a⋮7\\b⋮7\end{matrix}\right.\)
Mà a-b chia hết cho 7 => a,b đều chia hết cho 7 => a=b=7 (vì a,b là số nguyên tố)
=>\(49+5.7.7+49=343=7^3\Rightarrow c=3\)
Vậy a=b=7,c=3
7,\(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{49}-\frac{1}{50}=\left(1+\frac{1}{3}+...+\frac{1}{49}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{50}\right)\)
\(=\left(1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{50}\right)-2\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{50}\right)\)
\(=1+\frac{1}{2}+\frac{1}{3}+...+\frac{1}{50}-1-\frac{1}{2}-...-\frac{1}{25}\)
\(=\frac{1}{26}+\frac{1}{27}+...+\frac{1}{50}\left(đpcm\right)\)
10, \(n\left(n+1\right)\left(n+2\right)\left(n+3\right)=1680\)
<=>n(n+3)(n+1)(n+2)=1680
<=>(n^2+3n)(n^2+3n+2)=1680
Đặt n^2+3n+1=a (a thuộc Z), ta có:
(a-1)(a+1)=1680 <=> a^2-1=1680
<=>a^2=1681 <=> a = 41
=> \(n\left(n+3\right)+1=41\Leftrightarrow n\left(n+3\right)=40=5.8=-8.\left(-5\right)\)
Vậy n=5 hoặc n=-8