Cho góc nhọn α , tính giá trị của biểu thức
A=(3sinα+4cosα)2 + ( 4sinα-3cosα)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TH
1
Những câu hỏi liên quan
CM
10 tháng 12 2017
Vì tan α = 2 nên cos α ≠ 0
Ta có: G = 2 sin α + cos α cos α − 3 sin α = 2 sin α cos α + cos α sin α cos α cos α − 3 sin α cos α = 2 tan α + 1 1 − 3 tan α
Thay tan α = 2 ta được: G = 2.2 + 1 1 − 3.2 = − 5 5 = − 1
Vậy G = −1
Đáp án cần chọn là: D
DT
1
AH
Akai Haruma
Giáo viên
3 tháng 2 2021
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$P^2=(2\sin a+3\cos a)^2\leq (2^2+3^2)(\sin ^2a+\cos ^2a)=13$
$\Rightarrow P\leq \sqrt{13}$
Vậy $P_{\max}=\sqrt{13}$
Giá trị này đạt tại $\frac{\sin a}{2}=\frac{\cos a}{3}$
CM
8 tháng 10 2017
Vì tan α = 2 nên cos α ≠ 0 , chia cả tử và mẫu của P cho cos α ta được:
Ta có: P = 3 sin α − 5 cos α 4 cos α + sin α = 3 sin α cos α − 5 cos α cos α 4 cos α cos α + sin α cos α = 3. tan α − 5 4 + tan α
Thay tan α = 4 ta được: P = 3.4 − 5 4 + 4 = 7 8
Vậy P = 7 8
Đáp án cần chọn là: A
CM
21 tháng 8 2019
Đáp án A
P = s i n 2 90 ° − α + s i n 2 α = c o s 2 α + s i n 2 α = 1
DT
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Đặt \(A=sin\alpha+sin\left(90^0-\alpha\right)=sin\alpha+cos\alpha\)
\(\Rightarrow A^2=\left(sin\alpha+cos\alpha\right)^2\le2\left(sin^2\alpha+cos^2\alpha\right)=2\)
\(\Rightarrow A\le\sqrt{2}\)
\(A_{max}=\sqrt{2}\) khi \(\alpha=45^0\)
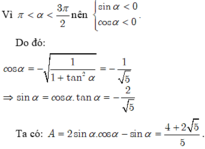
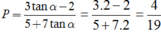
Ta dễ chứng minh \(sin^2a+cos^2a=1\) theo định lí Pytago
\(A=\left(3sina+4cosa\right)^2+\left(4sina-3cosa\right)^2\)
\(A=9sin^2a+24sina.cosa+16cos^2a+16sin^2a-24sina.cosa+9cos^2a\)
\(A=25sin^2a+25cos^2a=25\)
Arigato.<3