Cho tam giác ABC vuông tại A.đường cao AH,AC = 3cm,HC = 1,8cm.
a.Giải tam giác ABC
b.Tính độ dài phân giác AD của tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

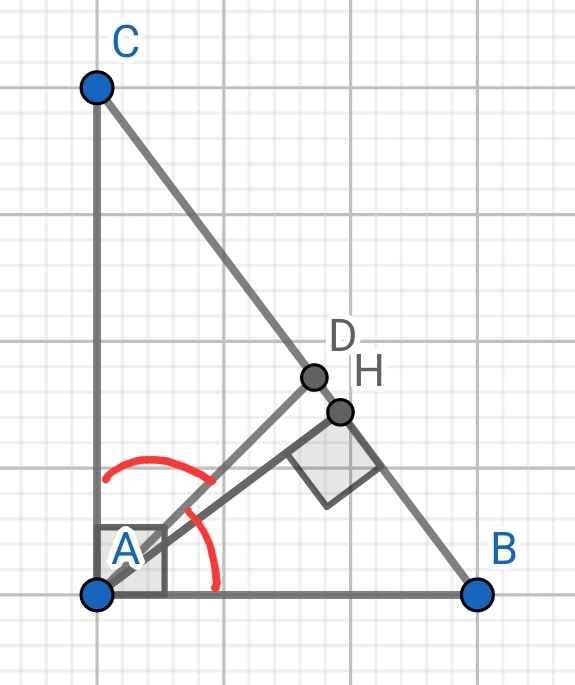
a) Xét hai tam giác vuông: ∆AHB và ∆CHA có:
∠B = ∠CAH (cùng phụ C)
⇒ ∆AHB ∽ ∆CHA (g-g)
⇒ AH/HC = HB/AH
⇒ AH.AH = HB.HC
⇒ AH² = HB.HC
Xét hai tam giác vuông: ∆ABC và ∆HAC có:
∠C chung
⇒ ∆ABC ∽ ∆HAC (g-g)
⇒ AC/HC = BC/AC
⇒ AC.AC = HC.BC
b) ∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 3² + 4²
= 25
⇒ BC = 5 (cm)
Do AD là tia phân giác của ∠BAC
⇒ BD/CD = AB/AC
⇒ AB/BD = AC/CD
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AB/BD = AC/CD = (AB + AC)/(BD + CD) = (3 + 4)/5 = 7/5
Do AB/BD = 7/5
⇒ BD = AB.5/7 = 3.5/7 = 15/7 (cm)

Xét ΔABC vuông tại A có AH là đường cao
nên AC^2=CH*CB
=>CB=3^2/1,8=5cm
AB=căn 5^2-3^2=4cm
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos\left(\dfrac{90}{2}\right)\)
\(=\dfrac{2\cdot3\cdot4}{3+4}\cdot cos45=\dfrac{12\sqrt{2}}{7}\left(cm\right)\)

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\)
Do đó: ΔHBA\(\sim\)ΔHAC
c: Ta có: ΔHBA\(\sim\)ΔHAC
nên HB/HA=HA/HC
hay \(HA^2=HB\cdot HC\)
d: Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
hay BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{5}{7}\)
Do đó: BD=15/7(cm); CD=20/7(cm)

a: BC=5cm
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
góc HBA=góc HAC
=>ΔHBA đồng dạng với ΔHAC
c: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
b)\(\text{Gọi DE⊥AB}\)\(\text{→DE//AC}\)
Vì AD là tia phân giác của tam giác ABC
\(\Rightarrow BAD=DAC=\dfrac{1}{2}BAC=45^0\)
\(\Rightarrow EAD=45^0\)
\(\Rightarrow TamgiácAEDvuôngcântạiE\)
\(\rightarrow AD=AE\sqrt{2}\)
Mak AD là tia phân giác
\(\dfrac{\Rightarrow DB}{DC}=\dfrac{AB}{AC}=\dfrac{4}{3}\)
Mak\(\dfrac{DB}{DC}=\dfrac{EB}{AE}\left(địnhlýTalet\right)\)
\(\dfrac{\Rightarrow EB}{AE}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{AE}{AE+EB}=\dfrac{3}{7}\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{3}{7}\Rightarrow AE=\dfrac{3}{7}.AB=\dfrac{12}{7}\)
\(\Rightarrow AD=AE.\sqrt{2}=\dfrac{12}{7}.\sqrt{2}=\dfrac{12\sqrt{2}}{7}\approx2,42\)
Xét tam giác ABC vuông tại A có AH đường cao
\(\Rightarrow AC^2=HC.BC\)
\(\Rightarrow BC=\dfrac{AC^2}{HC}=\dfrac{3^2}{1,8}=5\left(cm\right)\)
\(\Rightarrow HC=BC-HC=5-1,8=3,2\left(cm\right)\)
\(\Rightarrow AH^2=BH.HC\)
\(\Rightarrow AH^2=1,8.3,2=5,76\left(cm\right)\)
\(\Leftrightarrow AH=\sqrt{5,76}=2,4\left(cm\right)\)
\(\Rightarrow AB.AC=AH.BC\)
\(\Leftrightarrow AB=\dfrac{AH.BC}{AC}=\dfrac{2,4.5}{3}=4\left(cm\right)\)