Cho ứ giác ABCD cm
AB< BC+CD+AD
AC + BD < AB+BC+CD+AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NB
1
DD
Đoàn Đức Hà
Giáo viên
23 tháng 6 2021
a) Gọi \(O\)là giao điểm \(AC\)và \(BD\).
Theo bất đẳng thức tam giác ta có:
\(OA+OB>AB,OB+OC>BC,OC+OD>CD,OD+OA>AD\)
Cộng lại vế theo vế ta được:
\(2\left(OA+OB+OC+OD\right)>AB+BC+CD+DA\)
\(\Leftrightarrow AC+BD>\frac{1}{2}\left(AB+BC+CD+DA\right)\).
b) Theo bất đẳng thức tam giác:
\(AC< AB+BC,AC< CD+DA,BD< AB+DA,BD< BC+CD\)
Cộng lại vế theo vế ta được:
\(2\left(AC+BD\right)< 2\left(AB+BC+CD+DA\right)\)
\(\Leftrightarrow AC+BD< AB+BC+CD+DA\).
KC
0
26 tháng 11 2022
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
TP
0
NH
0
HH
1
TN
1 tháng 12 2016
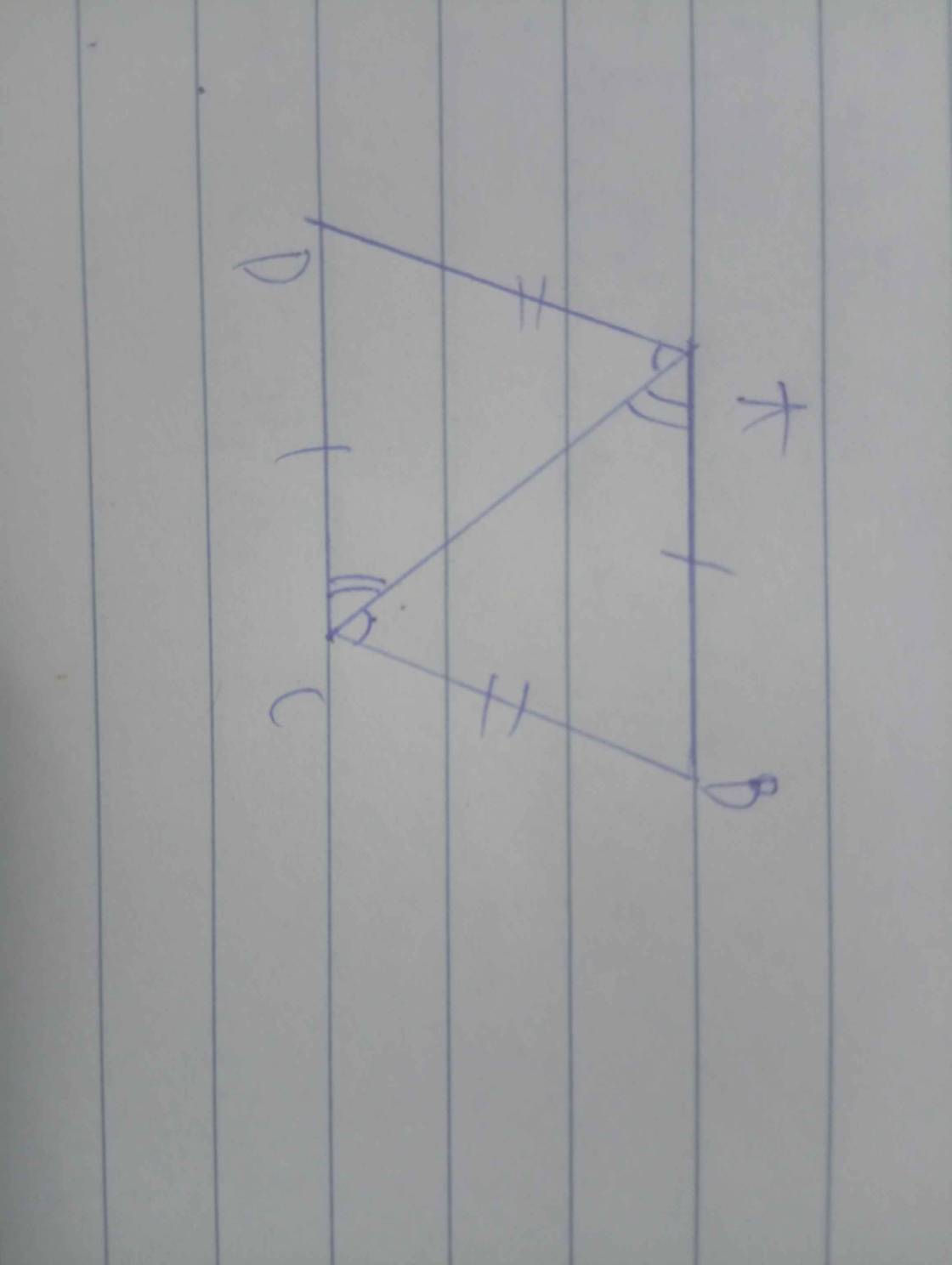
a) Gọi O la giao điểm AC và BD
ta có
AO+BO>AB ( bất đẳng thức trong tam giác AOB)
OC+OD>CD (bất đẳng thức trong tam giác OCD)
=> AO+BO+OC+OD>AB+CD
=>AC+BD>AB+CD
b) ta có
AO+OD >AD (bất đẳng thức trong tam giác AOD)
OC+OB >BC(bất đẳng thức trong tam giác BOC)
=>AO+OD+OC+OB>AD+BC
=> AC+BD>AD+BC
và 
. 
và 
.
thiếu đề bài
Cho tứ giác ABCD cm
CMR:
AB<NC+CD+AD
AC+BD<AB+BC+CD+AD
AB < OB + OA ; BC < OB + OC ; CD < OC + OD ; AD < OA + OD
=> AB +BC + CD + AD < 2(OA + OB + OC + OD)
=> (AB+BC+CD+AD)/2<AC+BD (1)
=> 2(AB + BC + CD + DA) > 2(AC + BD)
=> AB + BC + CD + DA > AC + BD (2)
Từ (1) và (2) suy ra đpcm
~hOK TỐT~
Câu hỏi của Nguyễn Tuấn Anh - Toán lớp 8 | Học trực tuyến
Tham khảo nhé,đề bài bạn còn thiếu gì không?