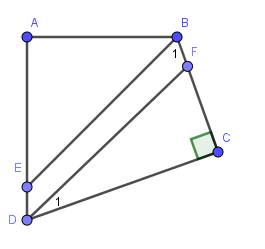
Cho tứ giác ABCD có góc A= góc C= 90 độ, tia phân giác góc B cắt cạnh CD ở E, tia phân giác của góc D cắt cạnh AB ở F. Chứng minh rằng BE // DF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 8 2023
Lời giải:
Theo định lý tổng 3 góc trong 1 tam giác:
Mà 2 góc này ở vị trí trong cùng phía nên
AH
Akai Haruma
Giáo viên
17 tháng 8 2021
Lời giải:
$\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0$
$90^0+\widehat{B}+90^0+\widehat{D}=360^0$
$\widehat{B}+\widehat{D}=180^0$
Theo định lý tổng 3 góc trong 1 tam giác:
$\widehat{DFB}=\widehat{D_1}+\widehat{C}=\frac{1}{2}\widehat{D}+90^0$
$\Rightarrow \widehat{B_1}+\widehat{DFB}=\widehat{B_1}+\frac{1}{2}\widehat{D}+90^0$
$=\frac{1}{2}\widehat{B}+\frac{1}{2}\widehat{D}+90^0$
$=\frac{1}{2}(\widehat{B}+\widehat{D})+90^0$
$=\frac{1}{2}.180^0+90^0=180^0$
Mà 2 góc này ở vị trí trong cùng phía nên $BE\parallel DF$
CM
2 tháng 11 2018
a) Ta có A E D ^ = E D C ^ v à A B F ^ = E D C ^ ⇒ D E / / B F (có góc ở vị trí đồng vị bằng nhau).
b) Từ câu a) suy ra DEBF là hình bình hành.
Ta có hình vẽ :
Tứ giác ABCD có : góc A = góc C = 90 độ nên : \(\hept{\begin{cases}\widehat{A}+\widehat{D}=180^o\Rightarrow\widehat{D}=90^o\\\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{B}=90^o\end{cases}}\)
=> Tứ giác ABCD là từ giác có 4 góc vuông => \(\hept{\begin{cases}\widehat{ADF}=\widehat{FDC}=45^o\\\widehat{ABE}=\widehat{EBC}=45^o\Leftrightarrow\widehat{BEC}=45^o\end{cases}}\Rightarrow\widehat{FDC}=\widehat{BEC}\)
Mà 2 góc này ở vị trí đồng vị => BE // DF ( điều phải chứng minh ).
Xin lỗi vẽ nhầm hình sữa điểm C và D đổi chỗ cho nhau nhé !!