Vẽ tam giác ABC có ba góc nhọn (AB NHỎ HƠN AC) , lấy diểm M nằm trên cạnh AB vẽ đoạn thẳng CM sao cho góc CMA = 70 độ. Hãy nêu tên 2 góc kề bù ? Tính góc BMC ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 7 2018
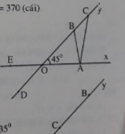
a) Có ba tam giác được tạo thành, đó là:
∆OAB,∆OAC,∆ABC.
b) Các góc kề bù với góc AOB là:
A O D ^ , B O E ^
A O B ^ và A O D ^ kề bù,
Nên A O B ^ + A O D ^ = 180 °
45 ° + A O D ^ = 180o; A O D ^ = 180 ° - 45 ° = 135 ° ;
Tương tự B O E ^ = 135 ° ;
c) Xảy ra hai trường hợp:
OC = 8 cm hoặc OC = 2 cm
20 tháng 5 2016
Với tài khoản VIP Luyện tập không giới hạn với hàng ngàn bài tập sinh động Đọc miễn phí hàng trăm số báo Toán tuổi thơ
2 tháng 7 2023
a: C nằm giữa A và B
=>CA+CB=AB
=>CB=4cm
b: C nằm giữa A và B
CA=CB
=>C là trung điểm của AB
LM
30 tháng 12 2020
xét tam giác ABM và tam giac AMD có
AB = AD ( gt)
AM chung
BM = MD ( M là trung điểm BD )
suy ra 2 tam giác bằng nhau
Hai góc kề bù : \(\widehat{CMA}\)và \(\widehat{CMB}\)
Do \(\widehat{CMA}\) và \(\widehat{CMB}\)là hai góc kề bù
\(\Rightarrow\widehat{CMA}+\widehat{CMB}=180^o\)( Tổng hai góc kề bù )
\(70^o+\widehat{CMB}=180^o\)
\(\Rightarrow\widehat{CMB}=180^o-70^o=110^o\)
Vậy \(\widehat{CMB}=110^o\) ( hay \(\widehat{BMC}=110^o\))