Cho hàm số y=f(x) có đạo hàm f’(x)=x2(x-1)(x+2)3(2-x) ∀xϵR. Số điểm cực trị hàm số đã cho bằng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
19 tháng 2 2017
Chọn đáp án B
Phương pháp
Số điểm cực trị của hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0.
Cách giải
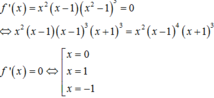
Tuy nhiên x=0 là nghiệm bội 2, x=1 là nghiệm bội 4 của phương trình f’(x)=0, do đó chúng không là cực trị của hàm số. Vậy hàm số có duy nhất 1 điểm cực trị x=-1.
Chú ý: HS nên phân tích đa thức f’(x) thành nhân tử triệt để trước khi xác định nghiệm, tránh sai lầm khi kết luận x=1 cũng là cực trị của hàm số.

CM
9 tháng 7 2018
Chọn C
Ta có 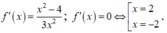
Nhận thấy f'(x) đổi dấu qua 2 nghiệm x = ± 2 nên hàm số y = f(x) có 2 điểm cực trị.








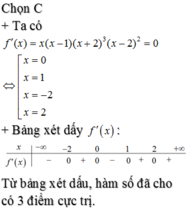
Ta thấy phương trình \(f'\left(x\right)=0\) có 3 nghiệm bội lẻ là \(x=\left\{1;-2;2\right\}\) nên hàm số đã cho có 3 điểm cực trị
Nghiệm bội chẵn không là cực trị.