Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90km trong một thời
gian đã định. Sau khi đi được 1 giờ người đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng
hẹn, người ấy phải tăng vận tốc thêm 4km/h. Tính vận tốc lúc đầu của người đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 7 2019
Đáp án A
Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).
Thời giạn dự định người đó đi hết quãng đường là 90/x (h).
Quãng đường người đó đi được sau 1 giờ là x (km).
Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).
Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).
Thời gian người đó đi hết quãng đường còn lại là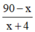 
(h).
Theo đề bài ta có phương trình:
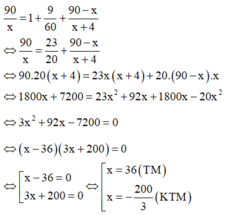
Vậy vận tốc lúc đầu của người đó là 36 km/h.
25 tháng 5 2015
Gọi x km là quãng đường AB (x>0)
Thời gian dự định đi: x/40 (h)
Quãng đường còn phải đi sau khi đã đi 1 giờ: x - 40 (km)
Vận tốc mới: 40 + 5 = 45 (km/h)
Thời gian đi đến B với vận tốc mới: (x - 40) / 45 (h)
15 phút = 1/4 h
Từ các kết quả trên ta có phương trình biểu diễn:
1 + (1/4) + {(x - 40) / 45} = (x/40)
( một giờ đi với vận tốc 40 km + 15 phút nghỉ + thời gian đi với vận tốc mới thì bằng thời gian dự định)
Sau khi quy đồng, khử mẫu và rút gọn ta sẽ có:
5x = 650
=> x = 130 (thỏa mãn)
=> Quãng đường AB dài 130 km.
1 tháng 6 2018
Cũng đang ôn thi sấp mặt luôn đây :)
Đưa được cái phương trình thôi còn lại bạn tự làm nha mai mình cũng thi rồi
\(\frac{90}{x}-1+\frac{3}{20}+\frac{90-x}{x+4}\)
Chúc thi tốt!!!!!!!!
13 tháng 5 2016
Gọi độ dài quãng đường AB là x (x>0) (km)
Vậy thời gian dự định người đó đi AB là x/50 (h)
Vậy quãng đường người đó đã đi là 2 x 50 = 100 (km)
Vậy quãng đường còn lại người đó phải đi là: x-100 (km)
Thời gian còn lại của người đó trên thực tế là: (x-100)/60 + 1/3 (h)
Ta có phương trình:
\(\frac{x-100}{60}+\frac{1}{3}=\frac{x-100}{50}\)
\(x=200\left(tmdk\right)\)
Vậy độ dài quãng đường AB là 200 km
26 tháng 1
Gọi vận tốc ban đầu của người đó là x(km/h)
(ĐIều kiện: x>0)
Thời gian dự kiến của người đó sẽ đi hết quãng đường là \(\dfrac{36}{x}\left(h\right)\)
Độ dài nửa quãng đường còn lại là: 36*1/2=18(km)
Thời gian đi nửa quãng đường đầu tiên là \(\dfrac{18}{x}\left(giờ\right)\)
vận tốc của người đó ở 18km còn lại là x+2(km/h)
Thời gian người đó đi hết 18km còn lại là \(\dfrac{18}{x+2}\left(h\right)\)
Theo đề, ta có phương trình:
\(\dfrac{18}{x}+\dfrac{18}{x+2}+\dfrac{3}{10}=\dfrac{36}{x}\)
=>\(\dfrac{18}{x+2}-\dfrac{18}{x}=-\dfrac{3}{10}\)
=>\(\dfrac{6}{x}-\dfrac{6}{x+2}=\dfrac{1}{10}\)
=>\(\dfrac{6x+12-6x}{x\left(x+2\right)}=\dfrac{1}{10}\)
=>\(\dfrac{12}{x\left(x+2\right)}=\dfrac{1}{10}\)
=>x(x+2)=120
=>\(x^2+2x-120=0\)
=>\(\left(x+12\right)\left(x-10\right)=0\)
=>\(\left[{}\begin{matrix}x+12=0\\x-10=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-12\left(loại\right)\\x=10\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc ban đầu là 10km/h
Thời gian xe lăn bánh trên đường là \(\dfrac{36}{10}=3,6\left(giờ\right)\)
Gọi vận tốc ban đầu của ng đó là v (km/h)
=> vận tốc lúc sau là v+4 (km/h)
Nếu đi vs vận tốc ban đầu thì thời gian để người đó đi hết quãng đg là:
t= 90/v (h)
Trong 1h ng đó đi đc:
v.1= v(km)
=> quãng đg còn lại là:
90-v (km)
=> thời gian để đi hết quãng đg còn lại là:
90-v/4+v (h)
Vậy nếu như đi ko theo dự tính thì thời gian tổng cộng đề người đó đi hết quãng đg là:
t= 1+0,5+ 90-v/4+v (h)
=> 90/v = 1+0,5+ 90-v/4+v
<=> 90v-v2-360-90v= -4,6v-1,15v2
<=>0,15v2+4,6v-360=0
<=> v= 36 (km/h)