các anh chị giải giúp em với ạ
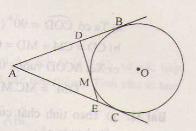
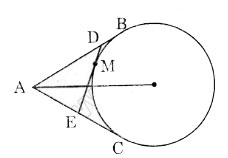
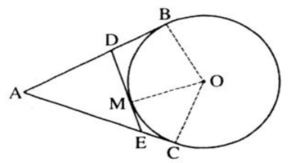
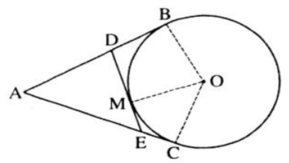
Từ điểm A ở bên ngoài một đườngtròn (C), kẻ các tiếp tuyến AB và AC với đường tròn ấy ( B,C là các tiếp điểm và B \(\ne\)C). điểm M thuộc cung nhỏ BC (M\(\ne\)B và M\(\ne\)C). gọi I,H,K lần lượt là hình chiếu vuông góc của M trên CB, BA,AC. biết MB cắt IH tại E, MC cắt IK tại F.
1) chứng minh bốn điểm M, K, I, C cùng thuộc một đường tròn
2) chứng minh MIK=MHI và MI2 =MH.MK
3) chứng minh EF vuông góc với MI.
4) đường tròn ngoại tiếp tam giác MFK và đường tròn ngoại tiếp tam giác MEH cắt nhau tại điểm thứ 2 là N. chứng tỏ khi M di động trên cung nhỏ BC(M\(\ne\)B, VÀ M \(\ne\)C) thì đường thẳng MN luôn đi qua một điểm cố định.