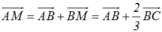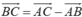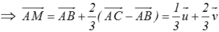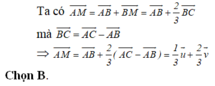Cho tam giác ABC có M là trung điểm AB, N là điểm trên cạnh AC sao cho AN = 2 NC. Gọi K là trung điểm MN. Hãy phân tích vectơ AK theo vectơ AB và vectơ AC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
15 tháng 5 2017
Theo các xác định điểm M, N ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB};\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.\)
Theo tính chất trung điểm của MN ta có:
\(\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\).
10 tháng 12 2020
a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??
MH
17 tháng 12 2023
a) Ta có:
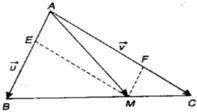
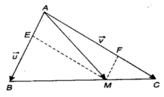
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+k\overrightarrow{BC}\)
\(=\overrightarrow{AB}+k\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
\(=\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\)
b) \(\overrightarrow{NP}=\overrightarrow{AP}-\overrightarrow{AN}\)
\(=\dfrac{2}{3}\overrightarrow{AC}-\dfrac{3}{4}\overrightarrow{AB}\)
Để \(AM\perp NP\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{NP}=\overrightarrow{0}\)
\(\Rightarrow\left[\left(1-k\right)\overrightarrow{AB}+k\overrightarrow{AC}\right]\left(-\dfrac{3}{4}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AC^2+\dfrac{2\left(1-k\right)}{3}\overrightarrow{AB}.\overrightarrow{AC}-\dfrac{3k}{4}\overrightarrow{AB}.\overrightarrow{AC}=\overrightarrow{0}\)
\(\Leftrightarrow\dfrac{3\left(k-1\right)}{4}AB^2+\dfrac{2k}{3}AB^2+\dfrac{1-k}{3}AB^2-\dfrac{3k}{8}AB^2=0\)
\(\Leftrightarrow AB^2\left[\dfrac{3\left(k-1\right)}{4}+\dfrac{2k}{3}+\dfrac{1-k}{3}-\dfrac{3k}{8}\right]=0\)
\(\Leftrightarrow18\left(k-1\right)+16k+8\left(1-k\right)-9k=0\left(AB>0\right)\)
\(\Leftrightarrow17k=10\)
\(\Leftrightarrow k=\dfrac{10}{17}\)