Giải dùm em bài này ạ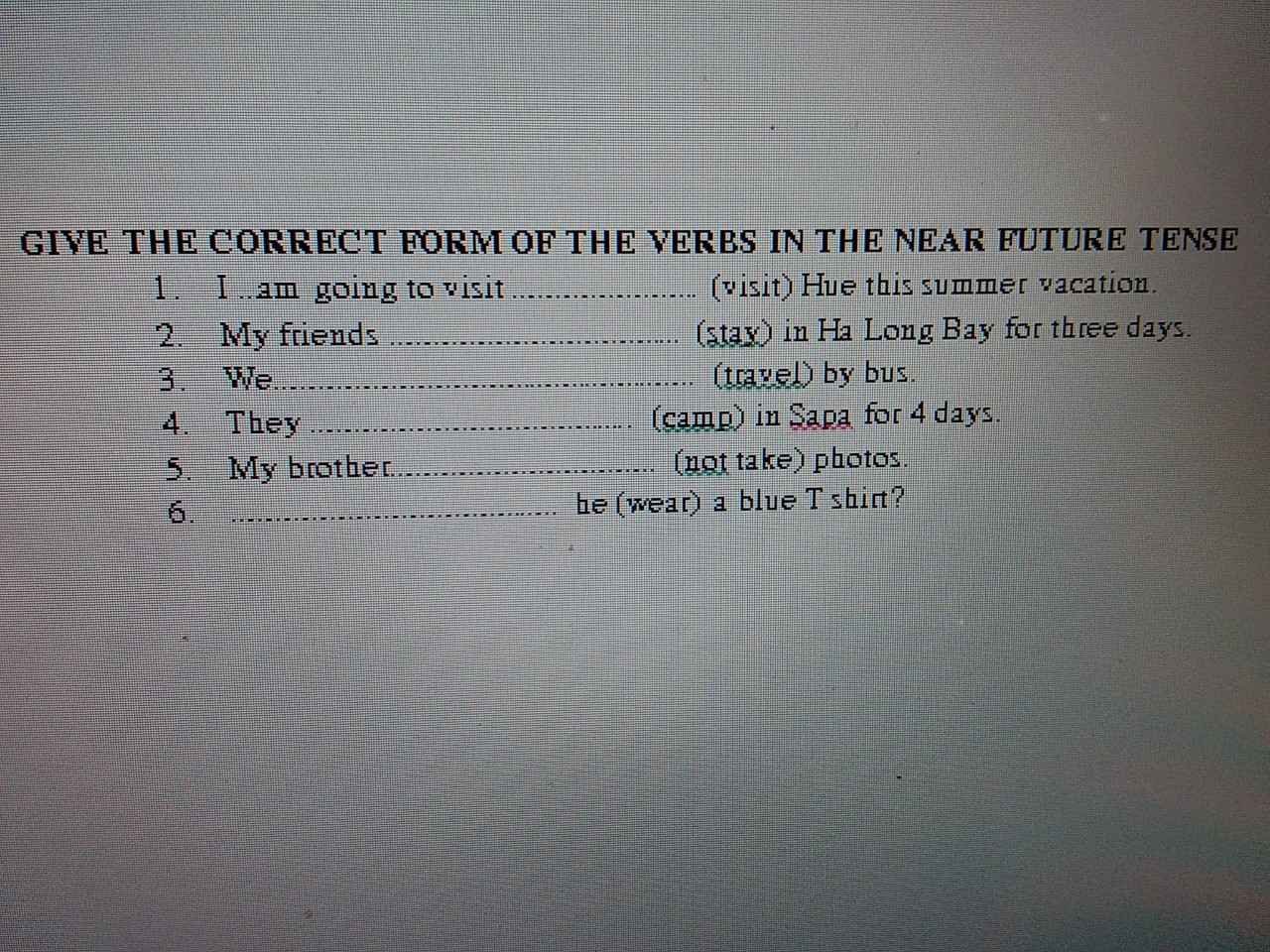
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
giải chi tiết 3 bài này dùm em vs ạ 
0
3 tháng 5 2018
\(\left(m+1\right)^2\ge4m\Leftrightarrow m^2+2m+1\ge4m\Leftrightarrow m^2-2m+1\ge0\)\(\Leftrightarrow\left(m-1\right)^2\ge0\)
Vì \(\left(m-1\right)^2\ge0\)(luôn đúng) nên pt vô số nghiêmj
Mình cũng ko bt đây là giải pt hay cm BĐT nữa nên nếu ko đúng mục đích thì bạn thông cảm
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
DN
3
23 tháng 11 2023
ĐKXĐ: \(\left\{{}\begin{matrix}5x^2+14x+9>=0\\x+1>=0\\x^2-x-20>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+1\right)\left(5x+9\right)>=0\\x+1>=0\\\left(x-5\right)\left(x+4\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< =-\dfrac{9}{5}\\x>=-1\end{matrix}\right.\\x>=-1\\\left[{}\begin{matrix}x>=5\\x< =-4\end{matrix}\right.\end{matrix}\right.\)
=>x>=5
\(\sqrt{5x^2+14x+9}-\sqrt{x^2-x-20}=5\sqrt{x+1}\)
=>\(\sqrt{5x^2+14x+9}-21+6-\sqrt{x^2-x-20}=5\sqrt{x+1}-15\)
=>\(\dfrac{5x^2+14x+9-441}{\sqrt{5x^2+14x+9}+21}+\dfrac{36-x^2+x+20}{6+\sqrt{x^2-x-20}}=5\left(\sqrt{x+1}-3\right)\)
=>\(\dfrac{5x^2+14x-432}{\sqrt{5x^2+14x+9}+21}+\dfrac{-x^2+x+56}{6+\sqrt{x^2-x-20}}=5\cdot\dfrac{x+1-9}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+54\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{x^2-x-56}{\sqrt{x^2-x-20}+6}=\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}\)
=>\(\dfrac{\left(x-8\right)\left(5x+4\right)}{\sqrt{5x^2+14x+9}+21}-\dfrac{\left(x-8\right)\left(x+7\right)}{\sqrt{x^2-x-20}+6}-\dfrac{5\left(x-8\right)}{\sqrt{x+1}+3}=0\)
=>\(\left(x-8\right)\left(\dfrac{5x+4}{\sqrt{5x^2+14x+9}+21}-\dfrac{x+7}{\sqrt{x^2-x-20}+6}-\dfrac{5}{\sqrt{x+1}+3}\right)=0\)
=>x-8=0
=>x=8(nhận)
AH
Akai Haruma
Giáo viên
24 tháng 11 2023
Lời giải:
\(P.\frac{1}{\sqrt{2}}=\frac{\sqrt{(x-1)+2\sqrt{x-1}+1}+\sqrt{(x-1)-2\sqrt{x-1}+1}}{\sqrt{(2x-1)+2\sqrt{2x-1}+1}-\sqrt{(2x-1)-2\sqrt{2x-1}+1}}\)
\(=\frac{\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}}{\sqrt{(\sqrt{2x-1}+1)^2}-\sqrt{(\sqrt{2x-1}-1)^2}}\)
\(=\frac{\sqrt{x-1}+1+\sqrt{x-1}-1}{\sqrt{2x-1}+1-(\sqrt{2x-1}-1)}=\frac{2\sqrt{x-1}}{2}=\sqrt{x-1}\)
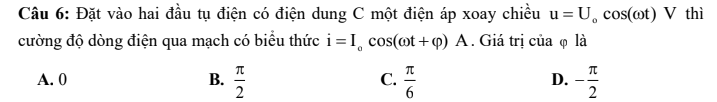
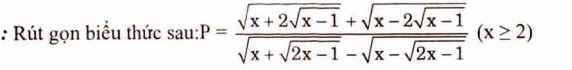
are going to stay
are going to travel
are going to camp
aren't going to take
Is he going to
Cho em hỏi là my brother là số ít hay số nhiều vậy chị