các bạn giải nốt hộ cái =))
Giải phương trình 2x^2−8x=−1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(8x+50=2x+30\\ \Rightarrow8x+50-2x-30=0\\ \Rightarrow6x+20=0\\ \Rightarrow6x=-20\\ \Rightarrow x=-\dfrac{10}{3}\)
\(8 x + 50 = 2 x + 30\)
\(⇒8x+50−2x−30=0\)
\(⇒6x+20=0\)
\(⇒6x=−20\)
\(⇒x=-\frac{10}{3}\)
HT

Điều kiện : x ≠ 2 và x ≠ -4
Ta có: 2 x x - 2 - x x + 4 = 8 x + 8 x - 2 x + 4 ⇔ 2x(x +4) –x(x -2) = 8x +8
⇔ 2 x 2 +8x – x 2 +2x = 8x +8
⇔ x 2 +2x -8 = 0
∆ ’ = 1 2 -1(-8) = 1 +8 = 9 > 0
∆ ' = 9 = 3
![]()
Cả hai giá trị của x đều không thỏa mãn điều kiện bài toán
Vậy phương trình đã cho vô nghiệm


Đặt t = 2 x (t > 0), ta có phương trình:
− t 3 + 2 t 2 + t – 2 = 0
⇔ (t − 1)(t + 1)(2 − t) = 0
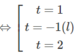
Do đó: 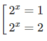

\(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(ĐKXĐ:x\ne-1,x\ne3\right)\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{2x\cdot2}{2\left(x+1\right)\left(x-3\right)}\)
\(\Rightarrow x\left(x+1\right)-x\left(x-3\right)=4x\)
\(\Leftrightarrow x^2+x-x^2+3x=4x\)
\(\Leftrightarrow x^2+x-x^2+3x-4x=0\)
\(\Leftrightarrow0x=0\)
Phương trình có vô số nghiệm , trừ x = -1,x = 3
Vậy ...
\(\dfrac{12x+1}{12}< \dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
\(\Leftrightarrow12\cdot\dfrac{12x+1}{12}< 12\cdot\dfrac{9x+1}{3}-12\cdot\dfrac{8x+1}{4}\)
\(\Leftrightarrow12x+1< 4\left(9x+1\right)-3\left(8x+1\right)\)
\(\Leftrightarrow12x+1< 36x+4-24x-3\)
\(\Leftrightarrow12x+1< 12x+1\)
\(\Leftrightarrow12x-12x< 1-1\)
\(\Leftrightarrow0x< 0\)
Vậy S = {x | x \(\in R\)}


2 2 x - 2 . 2 x + 8 < 2 3 x . 2 1 - x ⇔ 2 2 x + 2 . 2 x - 8 > 0
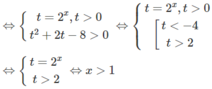

a:=>6x^2-8x+4x-6x^2<-4
=>-4x<-4
=>x>1
b: =>6x+8x^2-8x^2-24x>5
=>-18x>5
=>x<-5/18

a)\(6x^2-8x+2x\left(2-3x\right)< -4\)
\(\Leftrightarrow6x^2-8x+4x-6x^2< -4\)
\(\Leftrightarrow-4x< -4\)
\(\Leftrightarrow-4x.\dfrac{-1}{4}>-4\cdot\dfrac{-1}{4}\)
\(\Leftrightarrow x>1\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx>1\right\}\)
b)\(2\left(3x+4x^2\right)-8x\left(x+3\right)>5\)
\(\Leftrightarrow6x+8x^2-8x^2-24x>5\)
\(\Leftrightarrow-18x>5\)
\(\Leftrightarrow-18x\cdot\dfrac{-1}{18}< 5\cdot\dfrac{-1}{18}\)
\(\Leftrightarrow x< -\dfrac{5}{18}\)
Vậy bất phương trình có nghiệm là \(S=\left\{xIx< -\dfrac{5}{18}\right\}\)
Chia cả hai vế của phương trình \(2x^2-8x=-1\)cho 2 ta được phương trình
\(x^2-4x=-\frac{1}{2}\Leftrightarrow x^2-4x+4=-\frac{1}{2}+4\)
\(\Leftrightarrow\left(x-2\right)^2=\frac{7}{2}\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=\sqrt{\frac{7}{2}}\\x-2=-\sqrt{\frac{7}{2}}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2+\frac{\sqrt{14}}{2}\\x=2-\frac{\sqrt{14}}{2}\end{cases}}\)
Vậy phương trình có hai nghiệm là ....
4x2- 8x = -1
4x(x - 2) = -1