Năm hok này ,nếu đặt đc h/s tiên tiến thì bạn A sẽ đc ba thưởng cho một máy tình loại mới nhất co giá là 650000 đồng chưa kể giá trị gia tăng (VAT) . Học kì một vừa qua bạn A phấn đấu tốt và đặt loại...

YN

Yến Nguyễn Thị

9 tháng 5 2019

Năm hok này ,nếu đặt đc h/s tiên tiến thì bạn A sẽ đc ba thưởng cho một máy tình loại mới nhất co giá là 650000 đồng chưa kể giá trị gia tăng (VAT) . Học kì một vừa qua bạn A phấn đấu tốt và đặt loại giỏi nên ba bạn đã thưởng liền cho bạn ấy một máy tính cầm tay như đã hứa và cinf thưởng thêm cho ban A một quyển sách . Tổng 2 món quà của bạn A đc thưởng tính cả 10% thuế vat là 754600 đồng . Hỏi...

Đọc tiếp

#Toán lớp 8

1

KS

Kakarot Songoku

15 tháng 5 2019

Hỏi đáp Toán

Đúng(0)

DL

Đạt Lê Hồng

7 tháng 5 2019 - olm

Năm học này, nếu đạt được học sinh tiên tiến thì bạn A sẽ được ba thưởng cho một máy tính cầm tay loại mới nhất có giá 650000 đồng chưa kể thuế giá trị gia tăng (VAT). Học kì I vừa qua, bạn A phấn đấu tốt và đạt loại giỏi nên ba bạn đã thưởng liền cho bạn ấy một máy tính cầm tay như đã hứa và thưởng thêm cho bạn A một quyển sách. Tổng hai món quà mà bạn A được thưởng...

Đọc tiếp

#Toán lớp 8

1

HM

Hoàng Minh Hiếu

14 tháng 5 2019

29140 đồng

Đúng(0)

DL

dinh lê

3 tháng 5 2019 - olm

năm học này, nếu đạt được được học sinh tiên tiến thì bạn a sẽ được ba thưởng cho may tính cầm tay loại mới nhất có giá 650000đồng chưa kể thuế giá trị gia tăng (VAT). học kì I vừa qua, bạn A phấn đấu tốt và đạt loại giỏi nên ba bạn đã thưởng liền cho bạn ấy một máy tính cầm tay như đã hứa và còn thưởng thêm cho bạn A một quyển sách. Tổng hai món quà mà bạn A được...

Đọc tiếp

#Toán lớp 8

0

M

mimi

8 tháng 5 2019 - olm

giai song to cho 3 tkĐề thi học kì 2 môn Toán lớp 8 - Sở GD Bình Dương 2019Câu 3: Năm học này, nếu đạt được học sinh tiên tiến thì bạn A sẽ được ba thưởng cho một máy tính cầm tay loại mới nhất có giá 650000 đồng chưa kể thuế giá trị gia tăng (VAT). Học kì I vừa qua, bạn A phấn đấu tốt và đạt loại giỏi nên ba bạn đã thưởng liền cho bạn ấy một máy tính cầm tay như đã hứa và...

Đọc tiếp

#Toán lớp 8

0

NN

Nhok nhoi

3 tháng 5 2019

Năm học này, nếu đạt được học sinh tiên tiến thì bạn A sẽ được ba thưởng cho một máy tính cầm tay loại mới nhất có giá 650000 đồng chưa kể thuế giá trị gia tăng ( VAT). Học kì I vừa qua, bạn A phấn đấu tốt và đạt loại giỏi nên ba bạn đã thưởng liền cho bạn ấy một cái máy tính cầm tay như đã hứa và còn thưởng thêm cho bạn A một quyển sách. Tổng hai món quà mà bạn A được thưởng tính cả...

Đọc tiếp

#Toán lớp 8

1

KS

Kakarot Songoku

6 tháng 5 2019

Gọi x là giá của hai món đồ máy tính và sách(đ)(x>

Suy ra x.$\frac{10}{100}$ = $\frac{x}{10}$là thuế VAT

Lập pt:

x + $\frac{x}{10}$ = 754600

Giải ta được x = 686000(đ)

Giá của quyển sách là :

686000-650000 = 36000(đ0

Vậy giá của quyển sách là 36000đ

Đúng(0)

TT

Thanh Tam

5 tháng 5 2019

Năm học này, nếu đạt được hs tiên tiến thì bạn A sẽ được ba thưởng cho 1 máy tính cầm tay loại mới có giá 650.000 đồng chưa kể thuế giá trị gia tăng (VAT). Học kì I vừa qua, bạn A phấn đấu tốt và đạt loại giỏi nên ba bạn đã thưởng liền cho bạn ấy 1 máy tính cầm tay như đã hứa và còn thưởng thêm cho bạn A 1 quyển sách. Tổng 2 món quà mà bạn A được thưởng tính cả 10% thuế VAT là 754.600 đồng,...

Đọc tiếp

#Toán lớp 9

2

M

$Mr.VôDanh$

11 tháng 5 2019

đề thi toán hk2 trường em !

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

12 tháng 5 2019

Gọi giá sách chưa tính thuế là $x$ ngàn đồng

Giá máy tính và sách khi chưa tính thuế: $x+650$ ngàn

Theo bài ra ta có pt:

$\left(x+650\right)\left(1+\frac{10}{100}\right)=754,6$

$\Rightarrow x+650=686$

$\Rightarrow x=36$ ngàn đồng

Đúng(0)

CB

Cô Bé Lọ Lem

12 tháng 5 2019

1.Một tổ may sản xuất dự định làm 36 sản phẩm trong 1 ngày. Khi thực hện tổ còn vượt mức dự định 4 sản phẩm mỗi ngày. Vì vậy không những tổ đã hoàn thành công việc sớm 5 ngày và còn làm thêm được 4 sản phẩm nữa. Tính số sản phẩm mà tổ phải hoàn thành theo kế hoạch. 2.Năm học này, nếu đạt được học sinh tiên tiến thì bạn A sẽ được ba thưởng cho một máy tính cầm tay loại mới nhất có giá...

Đọc tiếp

#Toán lớp 8

2

KS

Kakarot Songoku

12 tháng 5 2019

Gọi x là số ngày mà tổ phải hoàn thành công việc theo kế hoạch (ngày,x > 0)

Suy ra x - 5 là số ngày mà tổ đã hoàn thành công việc sớm hơn dự định

Vì làm sớm hơn dụ định 5 ngày mà làm dư thêm 4 sản phẩm nên (36 + 4)(x - 5) -4 cũng là số sản phẩm dụ định cần làm của tổ

Lập PT:

36x = 40(x -5) - 4

Giải ta được x = 51

Nên số sản phẩm dụ định mà tổ phải chês tạo là 51 . 36 = 1836 (sản phẩm)

Vậy số sản phẩm mà tổ dự định làm là 1836 sản phẩm

Đúng(0)

KS

Kakarot Songoku

12 tháng 5 2019

2. Hỏi đáp Toán

Đúng(0)

MT

Minh tú Trần

25 tháng 12 2020 - olm

Ba bạn Nam mua một cái máy lạnh ở cửa hàng A hết 1150000 đồng ( đã tính thuế giá trị tăng VAT 10%).a) hỏi giá của cái máy lạnh khi chưa tính thuế giá trị tăng VAT là bao nhiêu ?b) Mẹ bạn Bình có "thẻ khách hàng thân thiết" ở cừa hàng A nên khi mua máy lạnh cùng loại ở của này, mẹ bạn Bình chỉ phải trả 9240000 đồng. hỏi khi có 'thẻ khách hàng thân thiết" thì khách hàng được giảm bao...

Đọc tiếp

#Toán lớp 8

0

NT

Nguyễn Thùy Chi

30 tháng 1 2021

Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng kể cả thuế giá trị gia tăng (VAT) với 10 % đối với loại hàng thứ nhất, 8% rồi vừa loại hàng thứ hai. Nếu thuê VAT đều là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng hai, 2,18 triệu đồng. Hỏi nếu không kể thuế VAT người đó phải trả bao nhiêu tiền cho mỗi loại...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 1 2021

Gọi x(triệu đồng) là số tiền người đó phải trả khi mua loại hàng thứ 1, y(triệu đồng) là số tiền người đó phải trả khi mùa loại hàng thứ 2(Điều kiện: $\left\{{}\begin{matrix}x\in Z^+\\y\in Z^+\end{matrix}\right.$)

Số tiền phải trả cho loại hàng thứ nhất kể cả thuế VAT 10% là: $\dfrac{11}{10}x$(triệu đồng)

Số tiền phải trả cho loại hàng thứ hai kể cả thuế VAT 8% là: $\dfrac{27}{25}y$(triệu đồng)

Vì khi mua hai loại hàng thì người đó phải trả tổng cộng 2,17 triệu đồng kể cả thuế VAT đối với 10% thuế VAT của loại hàng thứ nhất và 8% thuế VAT của loại hàng thứ hai nên ta có phương trình:

$\dfrac{11}{10}x+\dfrac{27}{25}y=\dfrac{217}{100}$

Số tiền phải trả cho mặt hàng thứ nhất kể cả thuế VAT 9% là:

$\dfrac{109}{100}x$(triệu đồng)

Số tiền phải trả cho mặt hàng thứ hai kể cả thuế VAT 9% là:

$\dfrac{109}{100}y$(triệu đồng)

Vì khi thuế VAT là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng nên ta có phương trình:

$\dfrac{109}{100}x+\dfrac{109}{100}y=\dfrac{218}{100}$(2)

Từ (1) và (2) ta lập được hệ phương trình:

$\left\{{}\begin{matrix}\dfrac{11}{10}x+\dfrac{27}{25}y=\dfrac{217}{100}\\\dfrac{109}{100}x+\dfrac{109}{100}y=\dfrac{218}{100}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0.5\\y=1.5\end{matrix}\right.$

Vậy: số tiền người đó phải trả cho loại thứ nhất là 500 nghìn đồng, loại thứ hai là 1,5 triều đồng.

Đúng(2)

PT

Pham Trong Bach

15 tháng 3 2018

Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng (VAT) với mức 10% đối với loại hàng thứ nhất và 8% đố với loại hàng thứ hai. Nếu thuế VAT ,là 9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho mỗi loại hàng?

#Toán lớp 9

2

CM

Cao Minh Tâm

15 tháng 3 2018

Giả sử giá của loại hàng thứ nhất và thứ hai không tính VAT lần lượt là x, y

(x, y > 0, triệu đồng; x < 2,17, y < 2,17)

Nếu áp dụng mức thuế VAT 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai thì :

+ Giá mặt hàng thứ nhất tính cả thuế VAT là: x + 10%.x = x + 0,1x = 1,1x

+ Giá mặt hàng thứ hai tính cả thuế VAT là: y + 8%.y = y + 0,08y = 1,08y.

Số tiền người đó phải trả là 2,17 triệu đồng nên ta có phương trình: 1,1x + 1,08y = 2,17 (1)

Nếu áp dụng mức thuế VAT 9% đối với cả hai loại hàng thì :

+ Giá mặt hàng thứ nhất tính cả thuế VAT là : x + 9%.x = x + 0,09x = 1,09x

+ Giá mặt hàng thứ hai tính cả thuế VAT là : y + 9%.y = y + 0,09y = 1,09y.

Số tiền người đó phải trả là 2,18 triệu đồng nên ta có phương trình:

1,09x + 1,09y = 2,18 ⇔ x+ y = 2 (2)

Từ (1) và (2) ta có hệ phương trình :

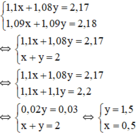
Giải bài 39 trang 25 SGK Toán 9 Tập 2 | Giải toán lớp 9

Vậy: nếu không kể thuế VAT thì người đó phải trả : 0,5 triệu cho loại thứ nhất và 1,5 triệu cho loại thứ hai .

Kiến thức áp dụng

Giải bài toán bằng cách lập hệ phương trình :

Bước 1 : Lập hệ phương trình

- Chọn các ẩn số và đặt điều kiện thích hợp

- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn

- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.

- Từ các phương trình vừa lập rút ra được hệ phương trình.

Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).

Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

Đúng(0)

T

Trần

23 tháng 1 2021

Hi

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP