Trong mặt phẳng với hệ tọa Oxy, cho Parabol (P): y=x2, điểm B(2;0), đường thẳng d: y=2x-3 và đường thẳng db: y=(2b-1)x-b2
1. viết phương trình đường thẳng đi qua điểm B và song song với đường thẳng d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 12 2020
Phần b mk chưa học nên chịu :v
a, Phương trình đường thẳng (d) là: y = ax + b
Vì đường thẳng (d) song song với đường thẳng y = 3x + 1 nên
\(\Rightarrow\) \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=3\\b\ne1\end{matrix}\right.\)
Với a = 3 ta được pt đường thẳng (d): y = 3x + b
Vì đường thẳng (d) đi qua điểm A(3;7) nên thay x = 3; y = 7 ta được:
7 = 3.3 + b
\(\Leftrightarrow\) b = -2 (TM)
Vậy phương trình đường thẳng (d) là: y = 3x - 2
Chúc bn học tốt!
23 tháng 4 2023
PTHĐGĐ là:
x^2-2x-m+2=0
Δ=(-2)^2-4(-m+2)
=4+4m-8=4m-4
Để (P) tiếp xúc (d) thì 4m-4=0
=>m=1
=>x^2-2x+1=0
=>x=1
=>y=1
31 tháng 1 2024
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
vậy: A(1;1); B(2;4)
Gọi H là tọa độ của hình chiếu vuông góc kẻ từ O xuống AB
O(0;0); H(x;y); A(1;1); B(2;4)
\(\overrightarrow{OH}=\left(x;y\right);\overrightarrow{AB}=\left(1;3\right)\)
Vì OH vuông góc với AB nên \(x\cdot1+y\cdot3=0\)
=>x+3y=0
Ta có: \(\overrightarrow{AH}=\left(x-1;y-1\right);\overrightarrow{AB}=\left(1;3\right)\)
mà A,H,B thẳng hàng
nên \(\dfrac{x-1}{1}=\dfrac{y-1}{3}\)
=>3x-3=y-1
=>3x-y=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-y=2\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y=6\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}10x=6\\x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\3y=-x=-\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(H\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Phương trình hoành độ giao điểm:
\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)
a. Khi \(m=-1\), (1) trở thành:
\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)
b.
\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m
Hay (d) cắt (P) tại 2 điểm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)
\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)
23 tháng 4 2023
PTHĐGĐ là:
x^2-2x-m+1=0
Δ=(-2)^2-4*1*(-m+1)
=4+4m-4=4m
Để (P) tiếp xúc (d) thì 4m=0
=>m=0
=>x^2-2x+1=0
=>x=1
=>y=1
CM
28 tháng 8 2018
Đáp án D
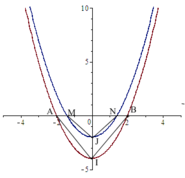
Phép tịnh tiến theo v → 0 ; b biến parabol P : y = x 2 − 4 thành parabol P ' : y = x 2 − 4 + b
Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là: − 2 ; 0 , 2 ; 0
Giao điểm M,N với Ox của (P) có toạn độ lần lượt là: − 4 − b ; 0 , 4 − b ; 0
Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt: 0 ; − 4 , 0 ; − 4 + b
Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:
I O . A B = 8 J O . M N ⇔ 4.4 = 8. 4 − b .2 4 − b ⇔ 4 − b 3 = 1 ⇔ b = 3 ⇒ J 0 ; − 1