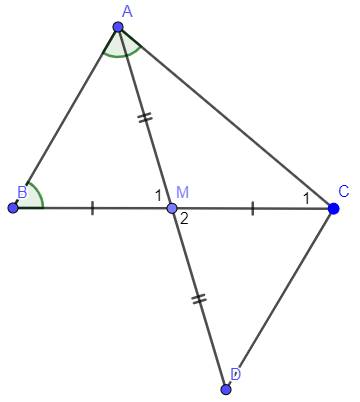
Cho tam giác ABC
a) Cho biết góc A= 80 độ, góc B= 60 độ. So sánh các cạnh của tam giác ABC
b) Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD. Chứng minh rằng: AB=CD và AB + AC > AD
c) Gọi N là trung điểm của đoạn thẳng CD và K là giao điểm của AN và BC. Chứng minh rằng: BC = 3CK
GIÚP MÌNH VỚI!!!!!!