Bài: cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Tính thể tích và diện tích xung quanh của chóp, biết:
a. Góc trong SB và đáy bằng 45°
b. Góc trong (SCD) và đáy bằng 60°
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SBA}\) là góc giữa SB và đáy
\(\Rightarrow\widehat{SBA}=45^0\Rightarrow SA=AB.tan45^0=a\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3}{3}\)
\(SB=SD=\sqrt{SA^2+AB^2}=a\sqrt{2}\)
\(S_{xq}=\dfrac{1}{2}SA.AD+\dfrac{1}{2}SA.AB+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=a^2\left(\sqrt{2}+1\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và đáy
\(\Rightarrow\widehat{SDA}=60^0\)
\(\Rightarrow SA=AD.tan60^0=a\sqrt{3}\)
\(V=\dfrac{1}{3}SA.AB^2=\dfrac{a^3\sqrt{3}}{3}\)
\(SB=SD=\sqrt{SA^2+AD^2}=2a\)
\(S_{xq}=\dfrac{1}{2}SA.AB+\dfrac{1}{2}SA.AD+\dfrac{1}{2}SB.BC+\dfrac{1}{2}SD.CD=3a^2\)

Đáp án A
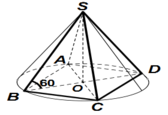
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)


Gọi O là tâm của hình vuông ABCD. Do S.ABCD là hình chóp đều nên SO ⊥(ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
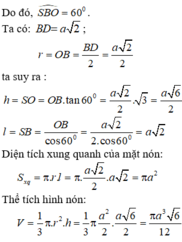

Đáp án D
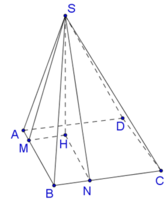
Gọi H là chân đường cao hạ từ S đến mặt phẳng (ABCD). Trong mặt phẳng (ABCD), kẻ HM,HN lần lượt vuông góc với AB,BC.

Vậy thể tích hình chóp S.ABCD là:
![]()

Lời giải:
$SA\perp (ABCD)$ nên $45^0=\angle (SB, (ABCD))=\angle (SB, AB)=\widehat{SBA}$
$\Rightarrow SA=AB=5$ (cm)
Thể tích khối chóp $S.ABCD$:
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}.5.5^2=\frac{125}{3}$ (cm3)
Đề bài thiếu 1 dữ liệu nữa (ví dụ SA vuông góc mặt đáy)