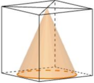
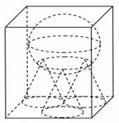
Một khối lập phương có cạnh 1m chứa đầy nước. Đặt vào trong khối đó một khối nón có đỉnh trùng với tâm một mặt của lập phương, đáy khối nón tiếp xúc với các cạnh của mặt đối diện. Tính tỉ số thể tích của lượng nước tràn ra ngoài và lượng nước ban đầu trong khối hộp.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 4 2019
Đáp án A.
Coi khối lập phương có cạnh 1.
Thể tích khối lập phương là V = 1
Từ giả thiết ta suy ra khối nón có chiều cao h=1, bán kính đáy r=1/2
Thể tích lượng nước trào ra ngoài là thể tích V1 của khối nón.
CM
24 tháng 12 2019
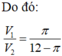
Đáp án B
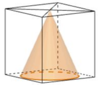
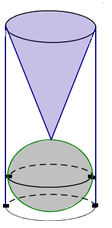
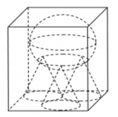
Gọi R,h lần lượt là bán kính đáy và chiều cao của khối trụ ⇒ h = 6 R = 6 . Thể tích của khối trụ là V = πR 2 h = π . 1 2 . 6 = 6 π . Khối cầu bên trong khối trụ có bán kính là R = 1 ⇒ V C = 4 3 π . R 3 = 4 3 π . Khối nón bên trong khối trụ có bán kính đáy là R = 1 và chiều cao h - 2R = 4. Suy ra thể tích khối nón là V N = 1 3 πR 2 h = 1 3 . π . 1 2 . 4 = 4 3 π . Do đó, thể tích lượng nước còn lại bên trong khối trụ là V 0 = V - V C + V N = 6 π - 2 . 4 π 3 = 10 π 3 . Vậy tỉ số cần tính là T = V 0 V = 10 π 3 : 6 π = 5 9 .
CM
20 tháng 1 2017
Chọn A.
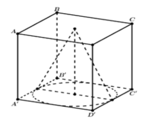
Lời giải. Ta có bán kính hình nón r= a 2 , đường cao h=a,
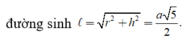
Diện tích toàn phần
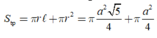
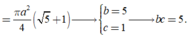
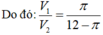
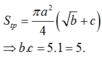
Thể tích khối lập phương là : 1^3=1 (m^3)
Thể tích lượng nước tran ra chính bằng thể tích khối chóp được đặt vào:
Thể tích khối chóp là:
\(\frac{1}{3}\pi R^2h\)=\(\frac{1}{3}.\pi.0,5^2.1=\frac{\pi}{12}\left(m^3\right)\)
Vậy tỉ số cần tìm là: \(\frac{\pi}{12}:1=\frac{\pi}{12}\)