Cho biểu thức V=(1x√+2+1x√−2)x√+2x√ với x>0,x≠0.
a) Rút gọn biểu thức V.
b) Tìm giá trị x của để V=13.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 10 2019
a, V = 1 x + 2 + 1 x − 2 x + 2 x = x − 2 + x + 2 x + 2 x − 2 x + 2 x = 2 x − 2
b, V = 1 3 ⇔ 2 x − 2 = 1 3 ⇔ x − 2 = 6 ⇔ x = 64 ( t / m )
CM
8 tháng 3 2018
Tìm được A = 24 5 và B = - 6 x - 4 với x > 0 và x ≠ 4 ta tìm được 0 < x < 1
Ta có M = - 1 + 2 x ∈ Z => x ∈ Ư(2) từ đó tìm được x=1
CM
8 tháng 1 2017
a) Ta có: 2x2 + 8 = 2(x2 + 4).
8 – 4x + 2x2 – x3
= (8 – x3) - ( 4x - 2x2)
= (2 – x).(4 + 2x + x2) - 2x.(2 - x)
= (2 – x).(4 + 2x + x2 – 2x)
= (2 - x). (4 + x2 )
* Do đó:
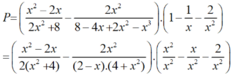
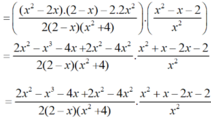
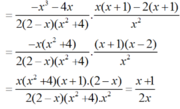
b) Tại x = 1 2 hàm số đã cho xác định nên thay x = 1 2 vào biểu thức rút gọn của P ta được:
PT
1
CM
26 tháng 11 2019
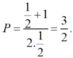
P = x − 2 x + 2 x − 1 x + 1 x + 2 , x > 0
P = x − 2 − x + 2 + x x x + 2 = x − 4 x x + 2 = x − 2 x