Cho nửa đường tròn (O) đường kính AB. Gọi M là điểm nằm trên nửa đường tròn. Xác định vị trí M sao cho chu vi tam giác MAB lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
28 tháng 10 2017
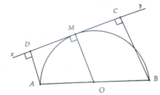
Ta có ABCD là hình thang vuông tại C và D
Mà O Là trung điểm AB và OM vuông góc với CD( tiếp tuyến của (O)
=> AD+BC=2OM=2R. Chú ý rằng CD ≤ AB (hình chiếu đường xiên)
=> S A B C D = 1 2 A D + B C . C D
= R.CD ≤ R.AB = 2 R 2
Do đó S A B C D lớn nhất khi CD=AB hay M là điểm chính giữa nửa đường tròn đường kính AB
b)Lấy C thuộc tia đối MA sao cho MC = MB => chi vi ABC = MA + MB + AB = MA + MC + 2R = AC + 2R.
=> Chu vi tam giác ABC lớn nhất <=> AC lớn nhất.
Xét tam giác MBC có góc BMC = 90độ và MC = MB(cách kẻ)
=> tam giác MBC vuông cân tại M => góc MCB = 45 độ
=> C thuộc cung chưa góc 45 độ dựng trên AB (1)
Lấy M' là điểm chính giữa nửa đường tròn đường kính AB (M' cùng phía với M).
Lấy D thuộc tia đối M'A sao cho M'D = M'A = M'B => AD = 2R
=> Ta cũng chứng minh được: D thuộc cung chứa góc 45độ dựng trên AB (2)
Từ (1) và (2) => C;D;A và B cùng thuộc 1 đường tròn.
Ta sẽ chứng minh được góc ABD = 90độ
=> AD là đường kính => AC ≤ AD (trong đường tròn đường kính là dây lớn nhất).
=> AC + 2R ≤ AD + 2R
=> AC + 2R ≤ 2R + 2R
=> AC + 2R ≤ 4R
=> Chu vi ABC ≤ 4R
Đạt được giá trị này <=> AC ≡ AD => M ≡ M'
=> M là điểm chính giữa nữa đường tròn đường kính AB