Từ đỉnh 1 thép chuông cao 26m, người ta nhìn thấy một tảng đá dưới góc 30 độ so với đường nằm ngang qua chân tháp. Hỏi khoảng cách giữa tảng đá với chân thác là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 4 2017
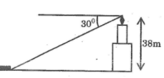
Khoảng cách từ đảo đến chân cột đèn biển là cạnh kề với góc 30 ° , chiều cao của cột đèn biển là cạnh đối diện với góc 30 °
Vậy khoảng cách từ đảo đến chân đèn là:
38.cotg 30 ° ≈ 65,818 (cm)
CM
30 tháng 1 2018
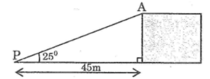
Chiều cao của vách đá là cạnh góc vuông đối diện với góc 25 °
Khi đó chiều cao của vách đá là:
45.tg 25 ° ≈ 20,984 (m)
14 tháng 10 2018
*gọi: A là đỉnh ngọn đèn biển; B là chân đèn; C là hòn đảo
>>tam giác ABC vuông tại B có: AB=38m; góc ACB=30 độ
>>khoảng cách từ đảo đến chân đèn:
AC=AB/tan30=38/tan30=38căn3=65,8179m
16 tháng 11 2021
a)Qũy đạo của hòn đá: \(y=25+v_0sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
Thời gian chuyển động của hòn đá:
\(\Rightarrow0=25+v_0\cdot sin\alpha\cdot t-\dfrac{1}{2}gt^2\)
\(\Rightarrow0=25+15\cdot sin30\cdot t-\dfrac{1}{2}\cdot10\cdot t^2\)
\(\Rightarrow t\approx3,11s\)
b)Khoảng cách từ chân tháp đến chỗ rơi:
\(S=x=v_0\cdot cos\alpha\cdot t\)
\(\Rightarrow S=15\cdot sin30\cdot3,11=23,325m\)
c)Ta có: \(v_x=v_0\cdot cos\alpha\)
\(v_y=v_0\cdot sin\alpha-gt\)
Vận tốc hòn đá lúc chạm đất:
\(v=\sqrt{(v_0\cdot sin\alpha)^2+\left(v_0\cdot sin\alpha-gt\right)^2}\)
\(=\sqrt{\left(15\cdot sin30\right)^2+\left(15\cdot sin30-10\cdot3,1\right)^2}\)
\(\approx24,7\)m/s
VT
21 tháng 9 2023
ở trên cho vx=v0⋅cosα sao xuống dưới chuyển thành sin rồi, v của bài này là 26,94 m/s ấy.
16 tháng 5 2022
Khoảng cách từ đảo đến chân đèn là:
\(38\cdot\cot30^0\simeq65,818\left(cm\right)\)
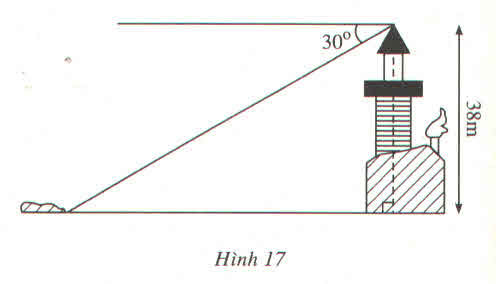
Đặt tam giác ABC vuông tại A với B là đỉnh tháp
Áp dụng tslg trong tam giác ABC vuông tại A:
\(tanC=\dfrac{AB}{AC}\)
\(\Rightarrow tan30^0=\dfrac{26}{AC}\)
\(\Rightarrow AC=\dfrac{26}{tan30^0}=26\sqrt{3}\left(m\right)\)