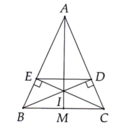
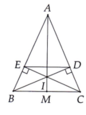
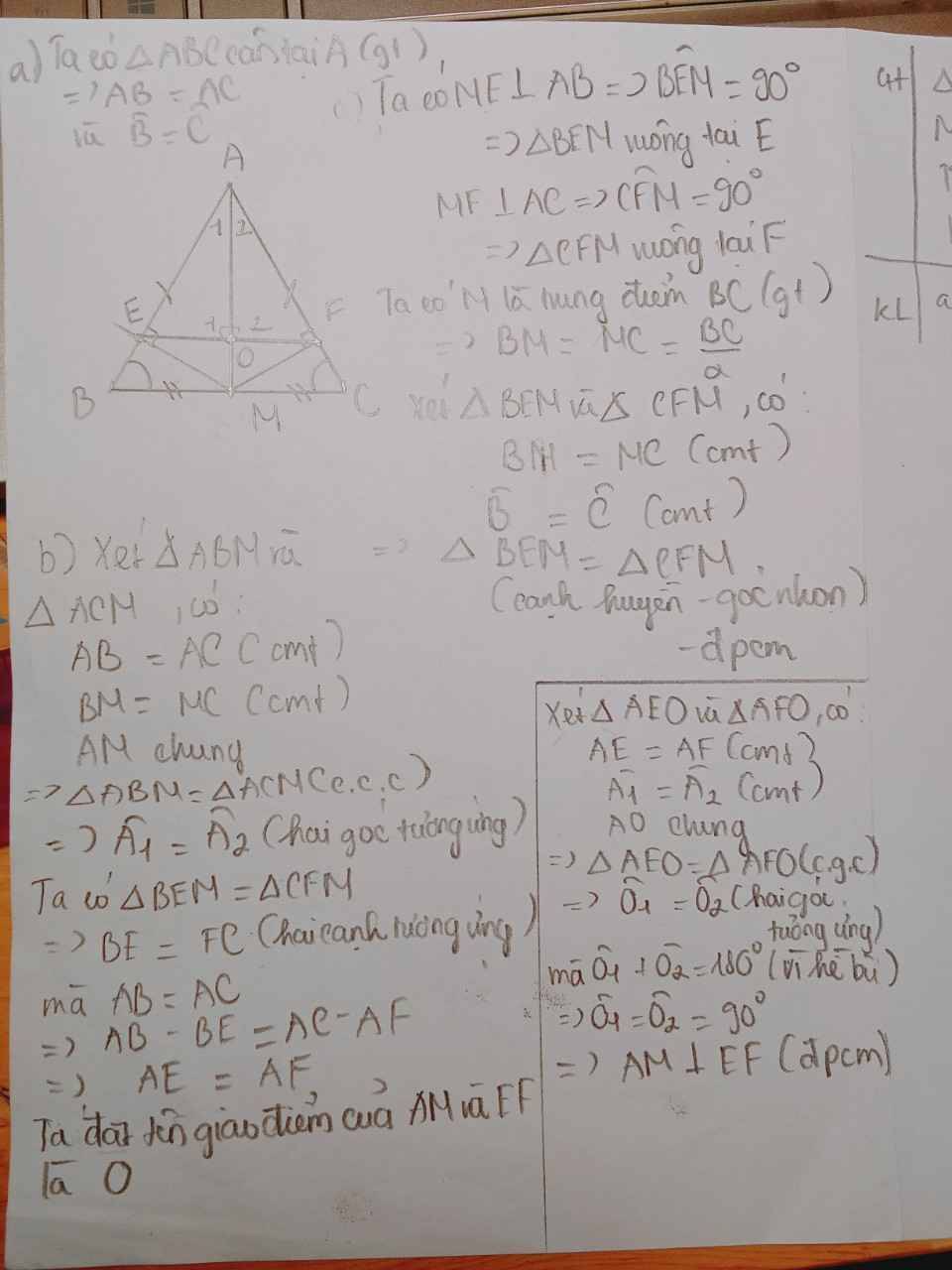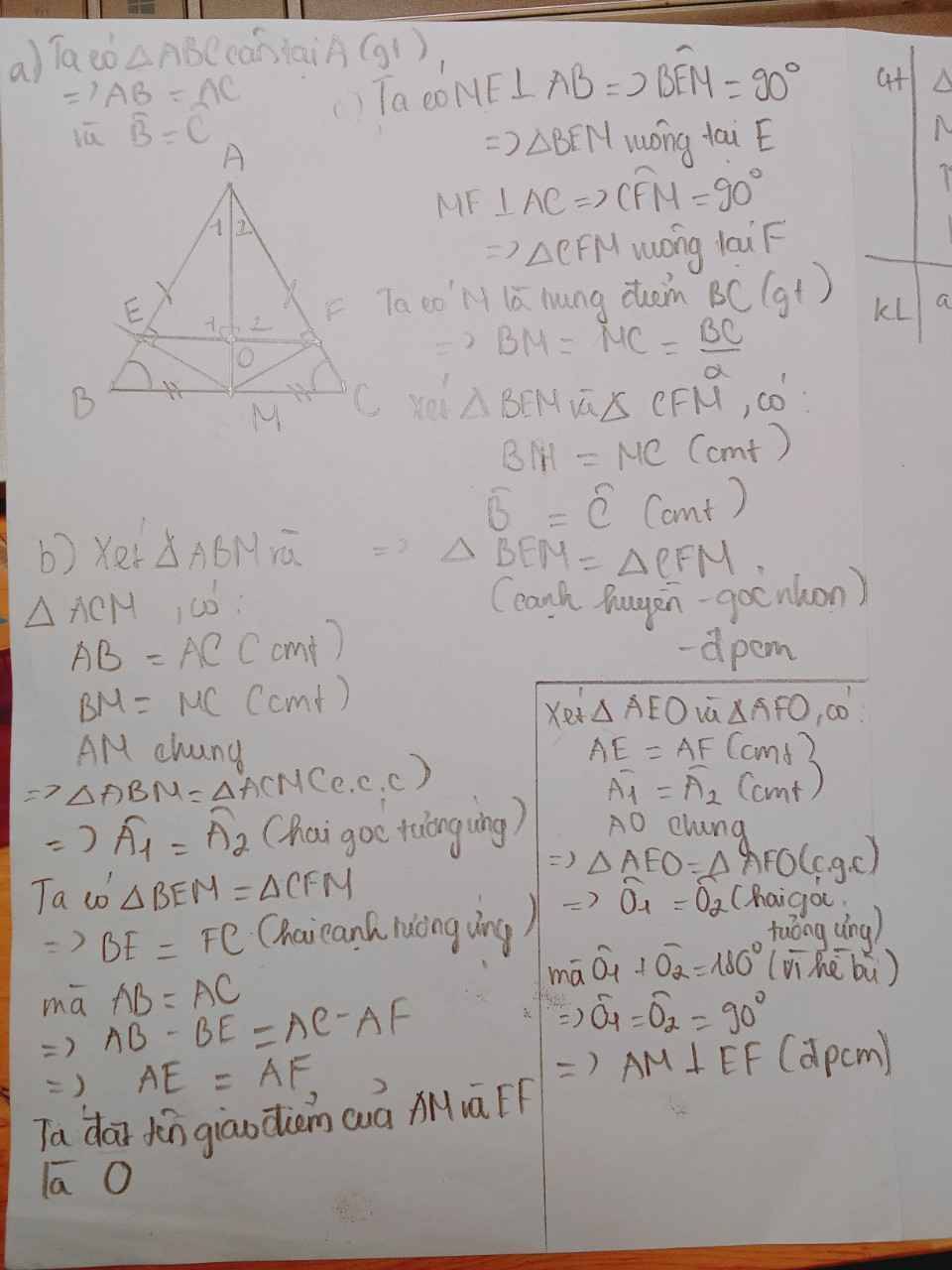Cho tam giác ABC có AM vuông góc với BC. Kẻ MD vuông góc với AB tại D. Kẻ ME vuông góc với AC tại E. Biết BD = CE, chứng minh tam giác ABC cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 2 2021
a) Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC(ΔABC cân tại A)
AM chung
Do đó: ΔAMB=ΔAMC(cạnh huyền-cạnh góc vuông)
Suy ra: MB=MC(hai cạnh tương ứng)
b) Ta có: ΔAMB=ΔAMC(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
c) Xét ΔDMB vuông tại D và ΔEMC vuông tại E có
MB=MC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDMB=ΔEMC(cạnh huyền-góc nhọn)
Suy ra: DM=EM(hai cạnh tương ứng)
Xét ΔMDE có MD=ME(cmt)
nên ΔMDE cân tại M(Định nghĩa tam giác cân)
15 tháng 12 2020
bạn không được nói vậy , nói thế là khinh người khác và đây là nơi chúng ta giao lưu giúp nhau mà , nên bạn không được nói bậy như thế.
6 tháng 3 2023
a: Xét ΔABD vuông tại D vaf ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
b: Xét ΔABC có AD/AC=AE/AB
nên DE//BC
c: Xét ΔIBC có góc ICB=góc IBC
nên ΔIBC cân tại I
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc BC
