Cho x,y là các số thực thõa thoả mãn 4x2+y2=1
Tìm GTLN và GTNN của M=\(\dfrac{2x+3y}{2x+y+2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow3x^2+2y^2+2z^2+2yz=2\)
\(\Rightarrow2\ge3x^2+2y^2+2z^2+y^2+z^2\)
\(\Leftrightarrow2\ge3\left(x^2+y^2+z^2\right)\)
Có: \(\left(x+y+z\right)^2\le3\left(x^2+y^2+z^2\right)\le2\)
\(\Rightarrow\)\(A^2\le2\) \(\Leftrightarrow A\in\left[-\sqrt{2};\sqrt{2}\right]\)
minA=-1\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x+y+z=-\sqrt{2}\\x=y=z\end{matrix}\right.\) \(\Rightarrow x=y=z=-\dfrac{\sqrt{2}}{3}\)
maxA=1\(\Leftrightarrow\left\{{}\begin{matrix}x+y+z=\sqrt{2}\\x=y=z\end{matrix}\right.\) \(\Rightarrow x=y=z=\dfrac{\sqrt{2}}{3}\)

Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự

| x - 2y | = 5
\(\Rightarrow\)\(\orbr{\begin{cases}x-2y=5\\x-2y=-5\end{cases}}\)
Theo bài ra : 2x = 3y = 5z
\(\Rightarrow\)\(\frac{2x}{30}=\frac{3y}{30}=\frac{5z}{30}\)
\(\Rightarrow\)\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)
\(\Rightarrow\)\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{3x}{45}=\frac{2y}{20}=\frac{2z}{12}=\frac{3x-2z}{45-12}=\frac{x-2y}{15-20}\)
+) với x- 2y = 5 thì \(\frac{x-2y}{15-20}=\frac{5}{-5}=-1\)\(\Rightarrow\frac{3x-2z}{45-12}=\frac{3x-2z}{33}=-1\)\(\Rightarrow3x-2z=-33\)
+) với x - 2y = -5 thì \(\frac{x-2y}{15-20}=\frac{-5}{-5}=1\)\(\Rightarrow\frac{3x-2z}{45-12}=\frac{3x-2z}{33}=1\)\(\Rightarrow3x-2z=33\)
Vậy GTLN của 3x - 2z là 33
\(2x=3y\Leftrightarrow x=\frac{3y}{2}\)
Vậy ...
\(\left|\frac{3y}{2}-2y\right|=5\)" thay \(x=\frac{3y}{2}\)vào "
\(\left|\frac{3y-4y}{2}\right|=5\)" quy đồng"
\(\left|\frac{-y}{2}\right|=5\)" rút gọn
Giá trị tuyệt đối với -y ta được:
\(\frac{y}{2}=5\Leftrightarrow y=10\)
Tương tự ta có :
\(x=\frac{5z}{2};2y=\frac{10z}{3}\)
\(\left|\frac{5z}{2}-\frac{10z}{3}\right|=5\Leftrightarrow\left|\frac{15z-20z}{6}\right|=5\Leftrightarrow\left|\frac{-5z}{6}\right|=5\)
Gía trị tuyệt đối với -5z âm ta được :
\(5z=30\Leftrightarrow z=6\)
Tương tự với x suy ra x = 15 "làm tắt "
Từ 1,2,3
Suy ra x = 15 ; y = 10 ; z = 6
Thay số ta được :
\(3.15-2.6=45-12=33\)

A = \(\frac{2x+3y}{2x+y+2}\)
<=> A(2x + y + 2) = 2x + 3y
<=> 2x.A + y.A + 2.A = 2x + 3y
<=> 2x(1 - A) + (3 - A).y = 2.A
Áp dụng BĐT Bunhia côp xki ta có: [2x.(1 - A) + ( 3 - A).y]2 < (4x2 + y2) .[(1 - A)2 + (3 - A)2]
=> (2.A)2 < 2A2 -8A + 10
<=> - 2A2 - 8A + 10 > 0
<=> A2 + 4A - 5 < 0
<=> (A - 1).(A + 5) < 0 <=> -5 < A < 1
Vậy Min A = -5 . giải hệ -5 = \(\frac{2x+3y}{2x+y+2}\); 4x2 + y2 = 1 => x ; y
Max A = 1 tại....

Đề thiếu. Bạn viết lại đề cẩn thận, rõ ràng để mọi người hỗ trợ tốt hơn bạn nhé.

Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
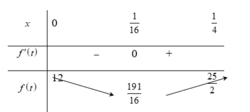
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
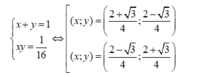
Chọn A.
Do \(4x^2+y^2=1\Rightarrow\) đặt \(\left\{{}\begin{matrix}x=\dfrac{sina}{2}\\y=cosa\end{matrix}\right.\)
\(\Rightarrow M=\dfrac{sina+3cosa}{sina+cosa+2}\Leftrightarrow M.sina+M.cosa+2M=sina+3cosa\)
\(\Leftrightarrow\left(M-1\right)sina+\left(M-3\right)cosa=-2M\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(M-1\right)^2+\left(M-3\right)^2\ge\left(-2M\right)^2\)
\(\Leftrightarrow2M^2+8M-10\le0\)
\(\Leftrightarrow-5\le M\le1\)
\(\Rightarrow\left\{{}\begin{matrix}M_{min}=-5\\M_{max}=1\end{matrix}\right.\)