giá trị nhỏ nhất của biểu thức F=y-x trên miền xác định bởi hệ \(\left[{}\begin{matrix}2x+y\le2\\x-y\le2\\5x+y\ge-4\end{matrix}\right.\)là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 1 2021
Con bạn bảo mk chỉ biết là Min F=1 khi x=2 và y=3
3 tháng 11 2023
\(\left(1\right)\Leftrightarrow y-2x\le2\Leftrightarrow\left\{{}\begin{matrix}x=0\Rightarrow y=2\\y=0\Rightarrow x=-1\end{matrix}\right.\Rightarrow F=3\\ \left(2\right)\Leftrightarrow2y-x\le4\Leftrightarrow\left\{{}\begin{matrix}x=0\Rightarrow y=2\\y=0\Rightarrow x=-4\end{matrix}\right.\Rightarrow F=6\\ \left(3\right)\Leftrightarrow x+y=5\Leftrightarrow\left\{{}\begin{matrix}x=0\Rightarrow y=5\\y=0\Rightarrow x=5\end{matrix}\right.\Rightarrow F=0\\ \Rightarrow MinF=3\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4).
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge - 1\) là nửa mp bờ \(d_4\), chứa điểm O.
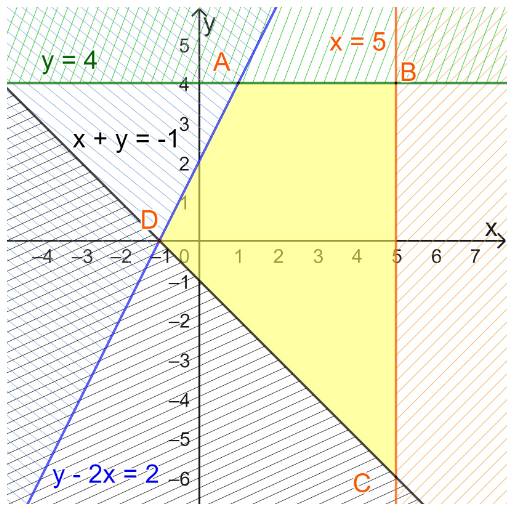
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = - 1 - 4 = - 5\)
\(F\left( {5;4} \right) = - 5 - 4 = - 9\)
\(F\left( {5;-6} \right) = - 5 - (-6) = 1\)
\(F\left( { - 1;0} \right) = - \left( { - 1} \right) - 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
Hàm có TXĐ là R khi và chỉ khi: \(\left(m-2\right)x^2+\left(m-2\right)x+4\ge0;\forall x\)
- Với \(m=2\) thỏa mãn
- Với \(m\ne2\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-2>0\\\Delta=\left(m-2\right)^2-16\left(m-2\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2\\\left(m-2\right)\left(m-18\right)\le0\end{matrix}\right.\) \(\Rightarrow2< m\le18\)
Kết hợp lại ta được: \(2\le m\le18\)
20 tháng 1 2021
Ta có: \(\left\{{}\begin{matrix}\left(m-1\right)x-y=2\\mx+y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)x+mx=2+m\\mx+y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(2m-1\right)=m+2\\mx+y=m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+2}{2m-1}\\y=m-mx=m-m\cdot\dfrac{m+2}{2m-1}=m-\dfrac{m^2+2m}{2m-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m+2}{2m-1}\\y=\dfrac{2m^2-m-m^2-2m}{2m-1}=\dfrac{m^2-3m}{2m-1}\end{matrix}\right.\)
Để x+y>0 thì \(\dfrac{m+2}{2m-1}+\dfrac{m^2-3m}{2m-1}>0\)
\(\Leftrightarrow\dfrac{m+2+m^2-3m}{2m-1}>0\)
\(\Leftrightarrow\dfrac{m^2-2m+2}{2m-1}>0\)
mà \(m^2-2m+2>0\forall m\)
nên 2m-1>0
\(\Leftrightarrow2m>1\)
hay \(m>\dfrac{1}{2}\)
Vậy: Để hệ phương trình có nghiệm duy nhất thỏa mãn x+y>0 thì \(m>\dfrac{1}{2}\)