 Mọi người giúp mik câu h,i bài 2; bài 3 với
Mọi người giúp mik câu h,i bài 2; bài 3 với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.2:
a: x^2-x+1=x^2-x+1/4+3/4
=(x-1/2)^2+3/4>=3/4>0 với mọi x
=>x^2-x+1 ko có nghiệm
b: 3x-x^2-4
=-(x^2-3x+4)
=-(x^2-3x+9/4+7/4)
=-(x-3/2)^2-7/4<=-7/4<0 với mọi x
=>3x-x^2-4 ko có nghiệm
5:
a: x^2+y^2=25
x^2-y^2=7
=>x^2=(25+7)/2=16 và y^2=16-7=9
x^4+y^4=(x^2)^2+(y^2)^2
=16^2+9^2
=256+81
=337
b: x^2+y^2=(x+y)^2-2xy
=1^2-2*(-6)
=1+12=13
x^3+y^3=(x+y)^3-3xy(x+y)
=1^3-3*1*(-6)
=1+18=19

\(\widehat{x'MC}=\widehat{xMN}\)(hai góc đối đỉnh
mà \(\widehat{xMN}=60^0\)
nên \(\widehat{x'MC}=60^0\)
Mz là phân giác của \(\widehat{x'MC}\)
=>\(\widehat{x'Mz}=\widehat{CMz}=\dfrac{60^0}{2}=30^0\)
Mz//Nt
=>\(\widehat{zMC}=\widehat{tNM}\)(hai góc đồng vị)
=>\(\widehat{tNM}=30^0\)
Nt là phân giác của góc y'NM
=>\(\widehat{y'NM}=2\cdot\widehat{tMN}=60^0\)

Bài 7:
a:
Ta có: ΔABC đều
=>AB=AC=BC và \(\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60^0\)
Xét ΔABC có \(\widehat{ACE}\) là góc ngoài tại đỉnh C
nên \(\widehat{ACE}=\widehat{CAB}+\widehat{CBA}=120^0\)
Xét ΔACE có \(\widehat{ACE}>90^0\)
nên AE là cạnh lớn nhất trong ΔACE
=>AE>AC
=>AE>AB
b: Xét ΔCAE có CA=CE(=BC)
nên ΔCAE cân tại C
=>\(\widehat{CAE}=\dfrac{180^0-120^0}{2}=30^0\)
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là phân giác của góc BAC
=>\(\widehat{HAC}=\dfrac{\widehat{BAC}}{2}=30^0\)
=>\(\widehat{HAC}=\widehat{CAE}\)
=>AC là phân giác của góc HAE
bài 9:
a: ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH\(\perp\)BC
b: Xét ΔAHM vuông tại H có AM là cạnh huyền
nên AM là cạnh lớn nhất trong ΔAHM
=>AM>AH
Xét ΔAHM có \(\widehat{AMB}\) là góc ngoài tại đỉnh M
nên \(\widehat{AMB}=\widehat{AHM}+\widehat{HAM}=90^0+\widehat{HAM}\)
=>\(\widehat{AMB}>90^0\)
Xét ΔAMB có \(\widehat{AMB}>90^0\)
nên AB là cạnh lớn nhất trong ΔAMB
=>AB>AM
=>AB>AM>AH
=>AC>AM>AH


Câu 4:
Xét tam giác ABC có
D là trung điểm của AC(gt)
E là trung điểm của BC(gt)
=> DE là đường trung bình của tam giác ABC
\(\Rightarrow AB=2DE=2.15=30\left(m\right)\)
Câu 5:
Xét hình thang ABCD có:
E là trung điểm của AD(gt)
F là trung điểm của BC(gt)
=> EF là đường trung bình của hình thang ABCD
\(\Rightarrow EF=\dfrac{AB+CD}{2}\Rightarrow45=\dfrac{32+x}{2}\Rightarrow x=45.2-32=58\left(cm\right)\)
Câu 6:
Xét hình thang AMEC có:
B là trung điểm AC(AB=BC)
BN//CE//AM( cùng vuông góc AD)
=> N là trung điểm ME
=> ME=2.MN=70(cm)
Xét hình thang BNFD có:
C là trung điểm BD(BC=CD)
CE//BN//DF(cùng vuông góc AD)
=> E là trung điểm NF
=> EF=EN=MN=35cm
Ta có: MF = EF+ME=70+35=105(cm)
Câu 5:
Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: \(EF=\dfrac{AB+CD}{2}\)
\(\Leftrightarrow x+32=90\)
hay x=58cm





 mọi người giúp mik bài 4 câu a vs ạ
mọi người giúp mik bài 4 câu a vs ạ 
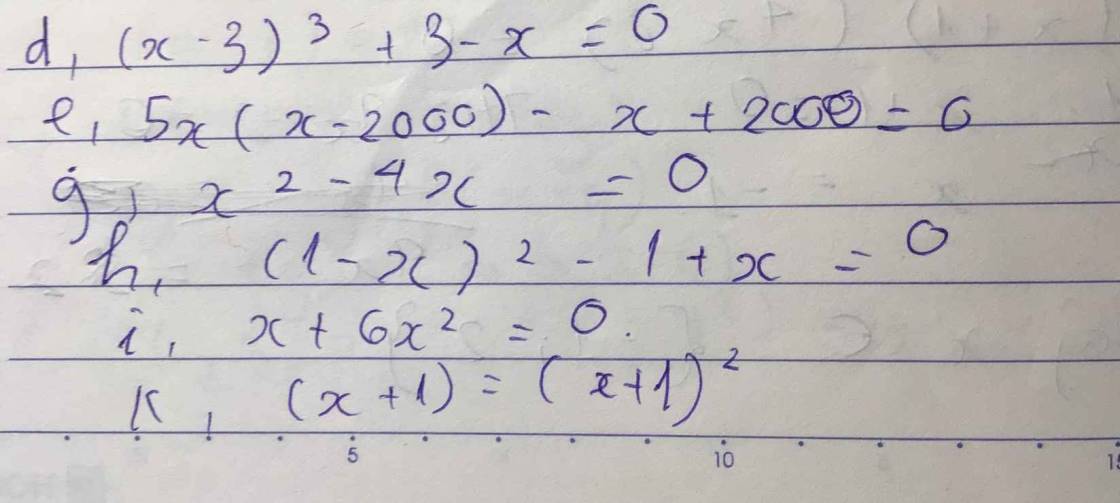

bài 2
h)
\(5^x+5^x.5^3=630\)
\(5^x\left(1+5^3\right)=630\)
\(5^x.126=630\)
\(5^x=5\)
x=1
bài 2
b) \(2/3\)\(.(-5/3)+11/3.-5/3\)
\(=(2/3+11/3).(-5/3)\)
\(=-65/9\)