Cho (P): y= x^2 + 1 và (d): y= 2x+3
a/ Vẽ (P) và (d)
b/ Tìm tọa độ giao điểm A, B của (P) và (d)
c/ Gọi C,D lần lượt là hình chiếu vuông góc của A, B lên Ox. Tính diện tích tứ giác ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DG
14 tháng 3 2018
Bác học lớp 9 phải ko bài này khá đơn giản mình thấy ai cũng làm đc chỉ cần độg não thui chứ bác hỏi thế rùi vô phòng thi thì sao lớp 9 phải tự học thui
12 tháng 1 2022
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2=2x+3\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{3;-1\right\}\\y\in\left\{9;1\right\}\end{matrix}\right.\)
b: A(3;9) B(-1;1)
\(OA=\sqrt{3^2+9^2}=3\sqrt{10}\)
\(OB=\sqrt{\left(-1\right)^2+1^2}=\sqrt{2}\)
\(AB=\sqrt{\left(-4\right)^2+\left(-8\right)^2}=4\sqrt{5}\)
\(\Leftrightarrow P=\dfrac{3\sqrt{10}+\sqrt{2}+4\sqrt{5}}{2}\)
\(S=\sqrt{\dfrac{3\sqrt{10}-\sqrt{2}+4\sqrt{5}}{2}\cdot\dfrac{3\sqrt{10}+\sqrt{2}+4\sqrt{5}}{2}\cdot\dfrac{-3\sqrt{10}+\sqrt{2}+4\sqrt{5}}{2}\cdot\dfrac{3\sqrt{10}+\sqrt{2}-4\sqrt{5}}{2}}\)
\(=\sqrt{\dfrac{576}{16}}=\dfrac{24}{4}=6\)
1 tháng 12 2023
a: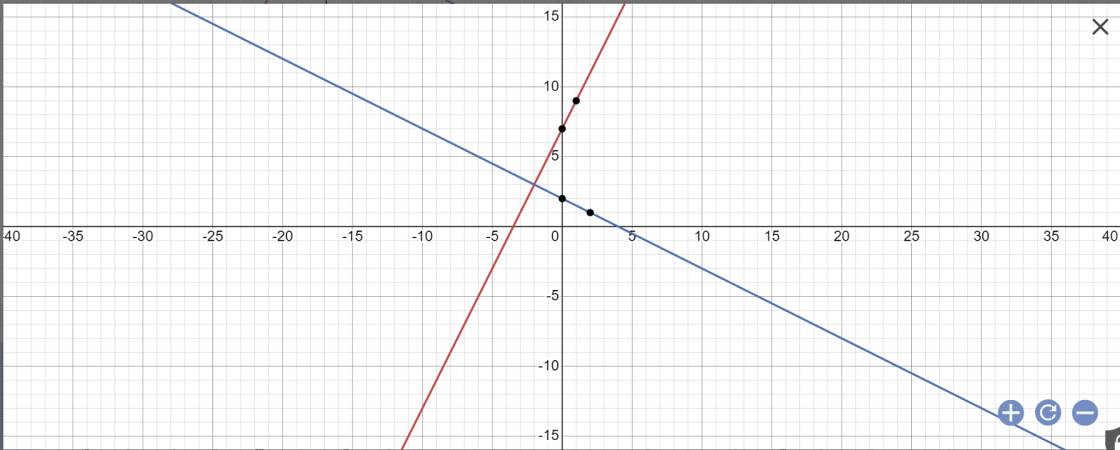 
b: Phương trình hoành độ giao điểm là:
\(2x+7=-\dfrac{1}{2}x+2\)
=>\(2x+\dfrac{1}{2}x=2-7=-5\)
=>2,5x=-5
=>x=-2
Thay x=-2 vào y=2x+7, ta được:
\(y=2\cdot\left(-2\right)+7=7-4=3\)
Vậy: A(-2;3)
c: Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x+7=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=-3,5\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=4\end{matrix}\right.\)
Vậy: C(4;0)
A(-2;3); B(-3,5;0); C(4;0)
\(AB=\sqrt{\left(-3,5+2\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\)
\(AC=\sqrt{\left(4+2\right)^2+\left(0-3\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+3,5\right)^2+\left(0-0\right)^2}=7,5\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
Xét ΔABC vuông tại A có \(sinABC=\dfrac{AC}{BC}=\dfrac{3\sqrt{5}}{7,5}\)
=>\(\widehat{ABC}\simeq63^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-63^0=27^0\)
d: Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC=\dfrac{3\sqrt{5}}{2}+3\sqrt{5}+7,5=\dfrac{9\sqrt{5}+15}{2}\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot\dfrac{3\sqrt{5}}{2}\cdot3\sqrt{5}=\dfrac{45}{4}\)
19 tháng 4 2023
PTHĐGĐ là:
x^2-2x-3=0
=>x=3 hoặc x=-1
=>A(3;9); B(-1;1)
d(A;Ox)=AD
=>D(3;0)
C là hình chiếu của B lên trục Ox nên C(-1;0)
=>ABCD là hình thang vuông
AD=9; BC=1; OD=3; OC=1
=>S ABCD=(9+1)*(3+1):2=20
27 tháng 7 2021
b) Phương trình hoành độ giao điểm là:
\(2x+6=-x+3\)
\(\Leftrightarrow2x+x=3-6\)
\(\Leftrightarrow3x=-3\)
hay x=-1
Thay x=-1 vào (d), ta được:
\(y=2\cdot\left(-1\right)+6=-2+6=4\)
Vậy: A(-1;4)