Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đạo hàm y’ = 3x2+6x+m. Ta có ∆ ' y ' = 9 - 3 m
Hàm số có cực đại và cực tiểu khi ∆ ' y ' = 9 - 3 m > 0 ⇔ m < 3
Ta có 
Gọi x1; x2 là hoành độ của hai điểm cực trị khi đó
Theo định lí Viet, ta có 
Hai điểm cực trị nằm về hai phía trục hoành khi y1.y2<0
Chọn C.
Đáp án D
Điều kiện để hai điểm cực trị nằm về hai phía của trục hoành PT y = 0 có ba nghiệm phân biệt. Xét PT
x 3 + 1 − 2 m x 2 + 2 2 − m x + 4 = 0 ⇔ x 3 + x 2 − 2 m x 2 + 2 m x + 4 x + 4 = 0 ⇔ x + 1 x 2 − 2 m x + 4 = 0
Để PT này có ba nghiệm phân biệt thì
Δ ' = m 2 − 4 > 0 − 1 2 − 2 m . − 1 + 4 ≠ 0 ⇔ m ∈ − ∞ ; − 2 ∪ 2 ; + ∞ m ≠ − 5 2
Chọn đáp án C.
Ta có y ' = 3 x 2 - 2 ( m + 1 ) x + m 2 - 2
trước tiên ta phải có phương trình y ' = 0 có hai nghiệm phân biệt
Điều kiện hai điểm cực trị của đồ thị hàm số nằm cùng về một phía đối với trục hoành là y x 1 . y x 2 > 0
⇔ y = 0 có đúng một nghiệm thực.
Thử trực tiếp các giá trị của m∈{−1,0,1,2} nhận các giá trị m∈{−1,0,2} để y = 0 có đúng một nghiệm thực.
Đáp án C
y ' = x 2 − 6 m x ; y ' = 0 ⇔ x 1 = 0 x 2 = 6 m .
Đồ thị hàm số có điểm cực đại, cực trị ⇔ y ' = 0 có hai nghiệm phân biệt ⇔ m ≠ 0 .
Các điểm cực trị nằm về hai phía của trục hoành ⇔ y 1 y 2 < 0
⇔ m − 36 m 3 + m < 0 ⇔ m 2 − 36 m 2 + 1 < 0 ⇔ m > 1 6 .
Chọn đáp án B
Hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là nghiệm của phương trình :
Để đồ thị hàm số đã cho có hai điểm cực trị nằm về hai phía của trục hoành
Phương trình (*) có hai nghiệm phân biệt khác 1
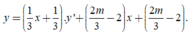
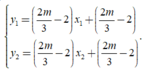
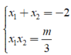
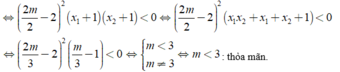
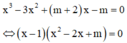
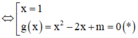
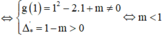
1/ \(y=x^3+3x^2+mx+m-2\)
\(y'=3x^2+6x+m\)
Chia đa thức \(y\) cho \(y'\) được phần dư là \(\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
\(\Rightarrow\)Phương trình đường thẳng \(d\) đi qua 2 cực trị có dạng:
\(y=\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
Gọi A là giao điểm của \(d\) với \(Ox\Rightarrow A\left(-1;0\right)\)
Đồ thị hàm số có 2 cực trị B, C nằm về 2 phía trục hoành khi và chỉ khi A nằm giữa B và C
\(\Rightarrow x_B< -1< x_C\) với \(x_B;x_C\) là nghiệm của pt \(f\left(x\right)=3x^2+6x+m=0\)
\(\Rightarrow3.f\left(-1\right)< 0\Leftrightarrow3\left(3-6+m\right)< 0\Rightarrow m< 3\)
Vậy với \(m< 3\) thì đồ thị hs có 2 cực trị nằm về 2 phía trục hoành
2/
\(y=x^3+3mx^2+m+1\Rightarrow y'=3x^2+6mx\)
Để hàm số có 2 cực trị \(\Rightarrow m\ne0\)
Chia đa thức \(y\) cho \(y'\) được phân dư \(-2m^2x+m+1\)
\(\Rightarrow\) phương trình đường thẳng \(d\) qua 2 cực trị có dạng:
\(y=-2m^2x+m+1\)
Để \(d\) song song đường thẳng \(y=-x+2017\)
\(\Rightarrow\left\{{}\begin{matrix}-2m^2=-1\\m+1\ne2017\end{matrix}\right.\) \(\Rightarrow m=\pm\dfrac{\sqrt{2}}{2}\)