Hai vật có khối lượng m1 m2 đặt cách nhau một khoảng R thì lực hấp dẫn giữa chúng có độ lớn là 16F. Thay đổi khoảng cách giữa chúng một lượng 15 (m) thì lực hấp dẫn giữa chúng có độ lớn là F. Tìm r
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
25 tháng 1 2021
\(F_{hd}=\dfrac{Gm_1m_2}{r^2}=1,334.10^{-7}\)
\(F_{hd}'=\dfrac{Gm_1m_2}{r'^2}=\dfrac{Gm_1m_2}{\left(r-5\right)^2}=5,336.10^{-7}\)
\(\Rightarrow\dfrac{F_{hd}}{F_{hd}'}=\dfrac{\left(r-5\right)^2}{r^2}=\dfrac{1334}{5336}\Rightarrow r=...\left(m\right)\)
\(\Rightarrow m_1m_2=\dfrac{5,336.10^{-7}.\left(r-5\right)^2}{G}=...\)
\(\left\{{}\begin{matrix}m_1m_2=...\\m_1+m_2=900\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m_1=...\left(kg\right)\\m_2=...\left(kg\right)\end{matrix}\right.\)
Hằng số G có trong SGK, bạn tự tìm
VT
28 tháng 4 2018
Chọn D.
Ta có: F h d = G m 1 m 2 r 2
Nếu khối lượng tăng gấp đôi → tử số tăng gấp 4; khoảng cách tăng gấp đôi → mẫu số tăng gấp 4. Lực hấp dẫn không thay đổi.
VT
7 tháng 2 2017
Đáp án D.
F h d = G m 1 m 2 r 2 khối lượng tăng gấp đôi → tử số tăng gấp 4; khoảng cách tăng gấp đôi → mẫu số tăng gấp 4. Lực hấp dẫn không thay đổi.
VT
26 tháng 9 2017
Chọn đáp án D
Ta có:
m1 + m2 = M
Lực hấp dẫn :
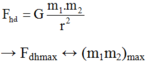
Áp dụng bdt cauchy cho hai số không âm ta có :
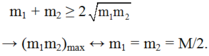
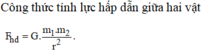
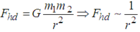
\(F_{hd0}=\dfrac{G.m_1.m_2}{R^2}\)=\(16F\)
\(F_{hd1}=\dfrac{G.m_1.m_2}{\left(R+15\right)^2}=F\)
lấy \(F_{hd0}\) chia \(F_{hd1}\)
\(\dfrac{16}{1}=\dfrac{\left(R+15\right)^2}{R^2}\)
\(\Leftrightarrow\dfrac{R+15}{R}=4\Rightarrow R=5m\)