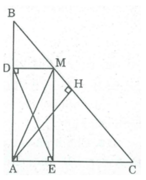
Cho tam giác ABC vuông tại A, M là trung điểm của đoạn BC. Gọi D, E lần lượt là chân các đường vuông góc kẻ từ M đến AB AC
1) tứ giác ADME là hình gì 2) kẻ AH vuông góc với BC. Chứng minh tứ giác DHME là hình thang cân
3) cho AB =6cm,AC=8cm .Tính diện tích tứ giác ADME và độ dài AH