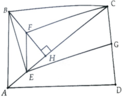
cho hình chữ nhật ABCD. Từ A vẽ AH vuông góc với BD (H thuộc BD). Gọi I,K,F theo thứ tự là trung điểm của AH,BH,CD.
a) Chứng minh KI song song với AB.
b) CM tứ giác DIKF là hình bình hành.
c) CM góc AKF = 90 độ.
d) Tính diện tích tam giác AKB biết AB =20cm, AD=15cm.
Em cần gấp lắm,mọi người giúp em nhé.