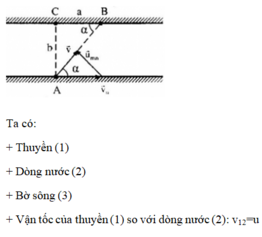
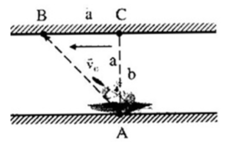
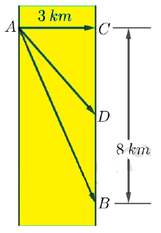
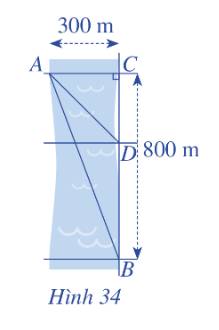
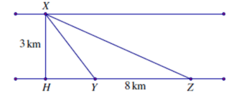
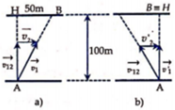
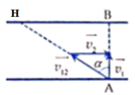
Ở một đoạn sông thẳng, dòng nước có vận tốc v0 , một người từ vị trí A ở bờ sông này muốn chèo thuyền tới vị trí B ở bờ sông bên kia. Cho AC = b, CB = a (C đối diện điểm A). Tính độ lớn nhỏ nhất của vận tốc thuyền so với nước mà người này phải chèo để tới được B.




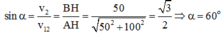
Giải:
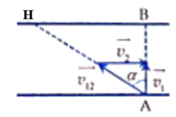
Theo đề ta có:
\(v_{23}=v^0\)
\(v_{13}=\sqrt{a^2+b^2}\)
\(\Leftrightarrow v_{13}=v_{12}+v_{23}\)
\(\Rightarrow v_{12}=\sqrt{a^2+b^2}-v^0\)
Vì \(v^0\) không đổi
Để \(v_{12}\) min thì \(\sqrt{a^2+b^2}\) min
\(\Leftrightarrow \) \(a^2+b^2\) min
Mà \(a^2+b^2\) \(\geq 2\) \(\sqrt{ab}\)
Dấu ''='' xảy ra khi
\(a=b\)
Vậy: \(v_{12}=a\sqrt{2}-v^0\)
\(\Leftrightarrow \)