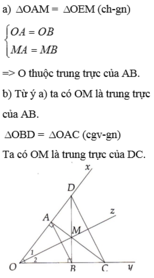
Cho đoạn thẳng AB hai đường thẳng d\(_1\) , d\(_2\) lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của AB.Một góc xOy có Ox cắt d\(_1\) tại C, Oy cắt d\(

HC

Hày Cưi

1 tháng 12 2018

Cho đoạn thẳng AB hai đường thẳng d\(_1\) , d\(_2\) lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của AB.Một góc xOy có Ox cắt d\(_1\) tại C, Oy cắt d\(_2\) tại D. Chứng minh rằng góc xOy vuông khi và chỉ khi đường tròn đường kính AB tiếp xúc với...

Đọc tiếp

#Toán lớp 9

0

HC

Hày Cưi

1 tháng 12 2018 - olm

Cho đoạn thẳng AB hai đường thẳng d\(_1\) , d\(_2\) lần lượt vuông góc với AB tại A và B. Gọi O là trung điểm của AB.Một góc xOy có Ox cắt d\(_1\) tại C, Oy cắt d\(_2\) tại D. Chứng minh rằng góc xOy vuông khi và chỉ khi đường tròn đường kính AB tiếp xúc với CD.

#Toán lớp 9

0

PT

Pham Trong Bach

16 tháng 10 2019

Cho góc xOy khác góc bẹt.a) Từ điểm M trên tia phân giác của góc xOy, kẻ các đường vuông góc MA, MB đến hai cạnh Ox, Oy (A thuộc Ox, B thuộc Oy), OM cắt AB tại H. Chứng minh A B ⊥ O M . b) Trên tia đối của tia Ox, Oy lần lượt lấy hai điểm C và D, sao cho OC = OD. Hai đương thẳng lần lượt vuông góc với Ox, Oy tại C và D cắt nhau ở E. Chứng minh ba điểm O, H, E thẳng...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

16 tháng 10 2019

Đúng(0)

FB

Florence Brittany

9 tháng 2 2020 - olm

Cho góc nhọn xOy. Gọi C là một điểm thuộc tia phân giác Oz của góc xOy. Kẻ CH vuông góc với Ox tại H, CK vuông góc với Oy tại K a) Chứng minh tam giác OHC = tam giác OKCb) Đường thẳng CH cắt tia Oy tại A, đường thẳng CK cắt tia Ox tại B. Chứng minh HB=KAc) Chứng minh HK // ABd) Góc xOy có số đo là bao nhiêu độ thì OA=AB ? Em hãy giải thích điều đó e) Gọi D là trung điểm của AB. Chứng minh ba điểm O,C,D...

Đọc tiếp

#Toán lớp 7

4

CM

Chu Mi Mi

9 tháng 2 2020

a, xét tam giác OCH và tam giác OCK có : OC chung

góc HOC = góc KOC do OC là phân giác của góc KOH (gT)

góc OHC = góc CKO = 90

=> tam giác OCK =tam giác OCH (ch-gn)

b, tam giác OCK =tam giác OCH (câu a)

=> CH = CK (đn)

xét tam giác HCB và tam giác KCA : có góc HCB = góc KCA (đối đỉnh)

góc BHC = góc AKC = 90

=> tam giác HCB = tam giác KCA (cgv-gnk)

=> HB = KA (đn)

c,CK = CH (Câu b)

=> tam giác CHK cân tại C (đn)

=> góc KHC = (180 - góc HCK) : 2 (tc) (1)

tam giác HCB = tam giác KCA (câu b) => CB = CA (đn)

=> tam giác CBA cân tại C (đn) => góc CAB (180 - góc BCA) : 2 (tc) (2)

góc HCK = góc BCA (đối đỉnh) (3)

(1)(2)(3) => góc KHC = góc CAB mà 2 góc này so le trong

=> HK // AB (tc)

d, có OH = OK do tam giác OCH = tam giác OCK (câu a)

HB = KA do tam giác HC = tam giác KCA (câu b)

OH + HB = OB

OK + KA = OA

=> OA = OB

=> tam giác OAB cân tại O (đn)

để OA = AB

<=> tam giác OAB đều (tc)

<=> góc xOy = 60

e, không biết làm em mới lớp 6

Đúng(0)

FB

Florence Brittany

9 tháng 2 2020

Ko sao đâu. Lớp 6 mà làm được như vậy là giỏi rồi em

Đúng(0)

PT

Pham Trong Bach

20 tháng 4 2018

Cho góc xOy khác góc bẹt Oz là tia phân giác của góc xOy. Gọi M là một điểm bất kì thuộc tia Oz. Qua M vẽ đường thẳng a vuông góc với Ox tại A, cắt Oy tại C và vẽ đường thẳng b vuông góc với Oy tại B, cắt Ox tại D. Chứng minh:a) Điểm O thuộc đường trung trực của AB;b) OM là đường trung trực của AB; Điểm M thuộc đường trung trực của...

Đọc tiếp

#Toán lớp 7

1

CM

Cao Minh Tâm

20 tháng 4 2018

Đúng(0)

DA

Đức Anh Lê

7 tháng 4 2023

cho 2 đt (O\(_1\);R\(_1\)) và (O\(_2\);R\(_2\)) với R\(_1\)>R\(_2\) tiếp xúc trong tại A. Đường thẳng O\(_1\)O\(_2\) cắt (O\(_1\);R\(_1\)) và (O\(_2\);R\(_2\)) lần lượt tại B và C khác A. Đường trung trực của BC cắt (O\(_1\);R\(_1\)) tại P và Q (D là trung điểm BC).1) chứng minh DP\(^2\)=R\(_1\)\(^2\)-R\(_2\)\(^2\)2) giả sử D\(_1\);D\(_2\);D\(_3\);D\(_4\) lần lượt là hình chiếu của D xuống các đường thẳng BP; PA; AQ; QB. Chứng minh...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 4 2023

1: \(O_2D=O_2A+CD=\dfrac{AC}{2}+\dfrac{BC}{2}=\dfrac{AB}{2}=R_1\)

góc O2MD=góc O2MC+góc CMD

=1/2*sđ cung CM+góc MCA

=90 độ

=>DM là tiếp tuyến của (O2)

PD^2=BD*DA=DC*BA=DM^2=O2D-R2^2

=>PD^2=R1^2-R2^2

2: Xet ΔD1BD vuông tại D1 và ΔD4BD vuông tại D4 có

BD chung

góc D1BD=góc D4BD

=>ΔD1BD=ΔD4BD

=>D1=D4

CM tương tự, ta được: DD2=DD3, BP=BQ, PA=PB

=>D1D+D2D+D3D+D4D<=1/2(BP+PA+AQ+QB)

=>2*(D1D+D2D)<=PA+PB

PB^2=BD^2+DP^2>=2*DB*DP

=>\(PB>=\dfrac{2\cdot DB\cdot DP}{PB}=2\cdot D_1D\)

Chứng minh tương tự,ta được: \(AP>=\dfrac{2\cdot DA\cdot DP}{PA}=2\cdot D_2D\)

=>ĐPCM

Đúng(0)

S

♡•꧁༺༒✰ŞŦΔŘ✰༒༺꧁•♡✿(➻❥𝒢𝑜𝓁𝒹❃𝒮𝓉𝒶𝓇✤) ❀

4 tháng 2 2021 - olm

Đề bài : Cho góc xOy nhọn , lấy điểm M thuộc tia phân giác của góc xOy . Từ M kẻ đường thẳng vuông góc với Ox cắt Ox tại A , Oy tại D và đường thẳng vuông góc với Oy cắt Oy tại B , Ox tại C. a ) Chứng minh : OA = OB b ) Chứng minh : Tam giác MCD cân . c ) Nếu góc xOy bằng 60 ° tam giác OCD là tam giác gì ? d ) Gọi N là trung điểm CD . Chứng minh 0 , M , N thẳng hàng .

#Toán lớp 7

0

P

phu

6 tháng 5 2018 - olm

cho góc xOy là góc nhọn .Kẻ tia phân giác Ot của góc xOy. lấy điểm A thuộc thía Ox , điểm B thuộc thìa Oy sao cho OA=OB. Qua A kẻ đường thẳng vuông góc với Ox cắt Ot tại C.a)chứng minh tam giác OAC=tam giác OBCb)chứng minh CB vuông góc với Oy và OC là đường trung trực của đoạn thẳng ABc)kéo dài đường thẳng BC cắt tia Ox tại D. so sánh BC và CDd)Qua B kẻ đường thẳng cuông góc với Ox tại I và cắt...

Đọc tiếp

#Toán lớp 7

0

N

NguyễnMai

5 tháng 3 2020 - olm

Cho góc xOy = 90 độ . Vẽ tia phân giác Oz của góc xOy . Trên tia Oz lấy điểm C. Qua C dựng đường thẳng vuông góc với Oz , cắt Ox , Oy lần lượt tại A và B. Gọi D và E lần lượt là trung điểm của OA và OB.

Chứng minh rằng :

a) ΔOAC và ΔBOC cân

b) C là trung điểm của AB

c) CE // Ox ; CD // Oy

d) CD ⊥ CE

#Toán lớp 7

0