Cho hình chóp S ABCD có đáy ABCD là hình bình hành.Gọi M N P lần lượt là trung điểm AB BC SO và O là giao điểm của AC và BD.Tìm giao tuyến của mặt phẳng (MNP) với các mặt của hình chóp S.ABCD nếu có.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
=>(SAD) giao (SBC)=xy, xy đi qua S, xy//AD//BC
b: Chọn mp(SBC) có chứa BC
\(P\in SC\subset\left(SBC\right)\)
\(P\in\left(MNP\right)\)
=>\(P\in\left(MNP\right)\cap\left(SBC\right)\)
mà NP//SB
nên (MNP) giao (SBC)=xy, xy đi qua P và xy//NP//SB
=>(MNP) giao (SBC)=PN
Gọi I là giao của PN với BC
=>I trùng với N

a: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: \(\left(SAB\right)\cap\left(SCD\right)=xy;S\in xy\);xy//AB//CD
b: Trong mp(ABCD), gọi I là giao điểm của MN với AD
\(I\in AD\)
\(I\in MN\subset\left(MNP\right)\)
Do đó: \(I=AD\cap\left(MNP\right)\)

- Ta có: S là điểm chung của hai mặt phẳng (SAD) và (SBC)
Từ S kẻ Sx sao cho Sx // AD // BC. Vậy Sx là giao tuyến của hai mặt phẳng (SAD) và (SBC).
- Ta có: M, P là trung điểm của SA, SD. Suy ra MP // AD // BC
Có: N là điểm chung của hai mặt phẳng (MNP) và (ABCD)
Từ N kẻ NQ sao cho NQ // AD.
Vậy NQ là giao tuyến của hai mặt phẳng (MNP) và (ABCD).

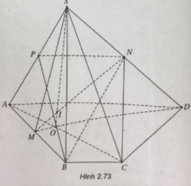
(h.2.73) a) Gọi O = AC ∩ MD Trong mặt phẳng (SMB) gọi I = SO ∩ MN.
Ta có: I = (SAC) ∩ MN
b) AD // BC (BC ⊂ (SBC))
⇒ AD // (SBC). Mặt phẳng (SAD) cắt mặt phẳng (NBC) theo giao tuyến NP // AD (P ∈ SA). Ta có thiết diện cần tìm là hình thang BCNP.
