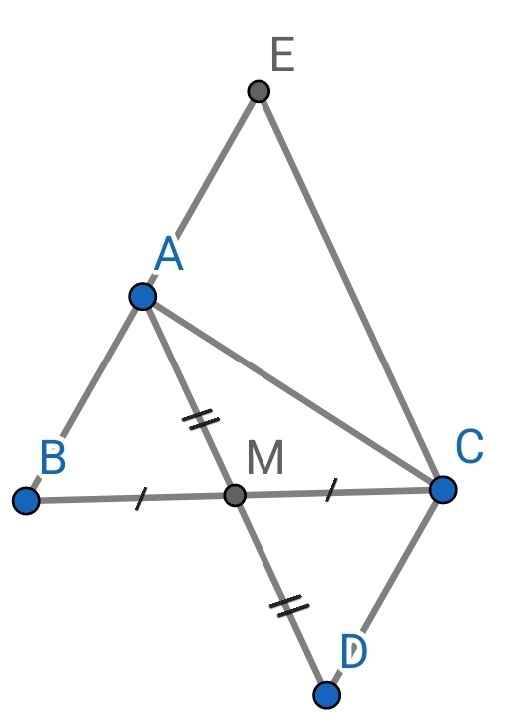
Cho tam giác ABC .Gọi M là trung điểm của BC ,qua điểm C vẽ đường thẳng song song với cạnh AB ,đường thẳng này cắt AM kéo dài tại D
A) chứng minh tam giác AMB = tam giác DMC
B)chứng minh BD song song với AC
C) gọi N là trung điểm của AB ,trên tia đối của tia NC lấy điểm E sao cho NE=NC .Chứng minh B là chung điểm của DE