K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

KV
7 tháng 1
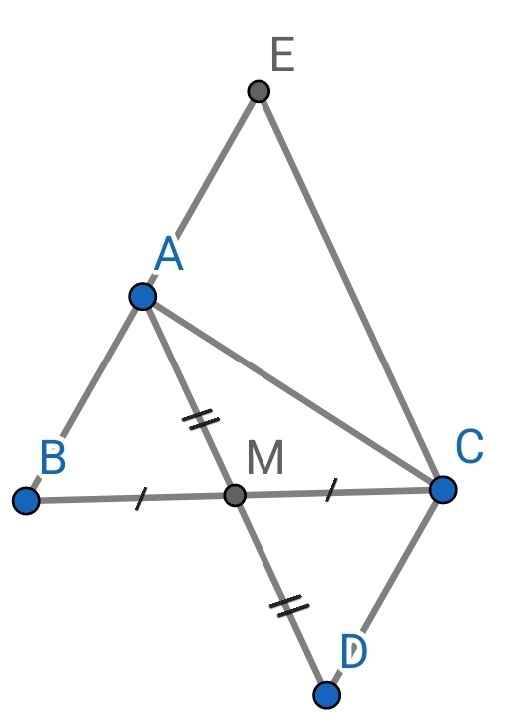 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = MC
Do M là trung điểm của AD (gt)
⇒ AM = MD
Xét ∆ABM và ∆DCM có:
AM = MD (cmt)
∠AMB = ∠CMD (đối đỉnh)
BM = MC (cmt)
⇒ ∆ABM = ∆DCM (c-g-c)
b) Do ∆ABM = ∆DCM (cmt)
⇒ ∠ABM = ∠CDM (hai góc tương ứng)
Mà ∠ABM và ∠CDM là hai góc so le trong
⇒ AB // CD
c) Do AB // CD (cmt)
⇒ ∠CAE = ∠ACD (so le trong)
∠ACE = ∠CAD (so le trong)
Xét ∆ACE và ∆CAD có:
∠ACE = ∠CAD (cmt)
AC là cạnh chung
∠CAE = ∠ACD (cmt)
⇒ ∆ACE = ∆CAD (g-c-g)
⇒ AE = CD (hai cạnh tương ứng)
Do ∆ABM = ∆DCM (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Mà AE = CD (cmt)
⇒ AB = AE
Vậy A là trung điểm của BE