Một vật được kéo trên mặt phẳng nghiêng với lực F, hệ số ma sát trượt = 0,2
Khối lượng m = 500g
g = 10m/s^2
Góc alpha = 60°
Gia tốc a = 10m/s^2. Tính lực kéo
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
18 tháng 11 2018
a) (2 điểm)
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật: (0,5 điểm)
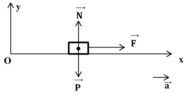
+ Viết phương trình định luật II Niu-tơn: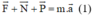 
(0,5 điểm)
+ Chiếu pt (1) lên trục Ox ta được: F = m.a (0,5 điểm)
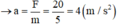(0,5 điểm)
b) (2 điểm)
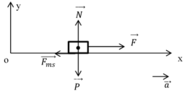
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật
+ Viết phương trình định luật II Niu-tơn
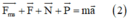(0,5 điểm)
+ Chiếu pt (2) lên trục Oy: N – P = 0
→ N = P = m.g = 5.10 = 50N (0,5 điểm)
+ Độ lớn lực ma sát: F m s = μ.N = 0,2.50 = 10N (0,5 điểm)
+ Chiếu pt (2) lên trục Ox: F – F m s = ma
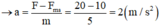(0,5 điểm)
HT
6 tháng 1 2021
a/ \(F_k-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k-m.a}{mg}=...\)
b/ \(F_k.\cos30^0-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k.\cos30^0-m.a}{mg}\)
VT
24 tháng 7 2017
Đáp án D
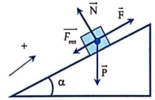
Vật chịu tác dụng của các lực: Lực kéo , trọng lực , phản lực của mặt phẳng nghiêng và lực ma sát .
Vì P.sinα = 15 N < F = 70 N nên vật chuyển động lên theo mặt phẳng nghiêng (được mặc nhiên chọn là chiều dương).
Công của từng lực:
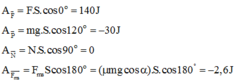
Tổng công của tất cả các lực tác dụng lên vật là
25 tháng 11 2018
sin\(\alpha=\dfrac{AH}{AB}\)\(\Rightarrow cos\alpha\)\(\approx0,74\)
150g=0,15kg
sau 5s kể từ lúc bắt đầu chuyển động vật đật v=20m/s
\(\Rightarrow a=\dfrac{v-v_0}{t}\)=4m/s2
theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\) (1)
chiếu (1) lên trục Ox phương song song với mặt phẳng, chiều dương cùng chiều chuyển động
F-\(\mu.N=m.a\) (2)
chiếu (1) lên trục Oy phương vuông gốc với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
N=cos\(\alpha.P=cos\alpha.m.g\) (3)
từ (2),(3)\(\Rightarrow\mu\approx\)0,187
Mong mn giúp e nhanh ạ
500g=0,5kg
theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox như hình
F-Fms=m.a (1)
chiếu lên trục Oy như hình
N=cos\(\alpha\).P (2)
từ (1),(2)\(\Rightarrow F-\mu.cos\alpha.P=m.a\)
\(\Rightarrow F=\)5,5N