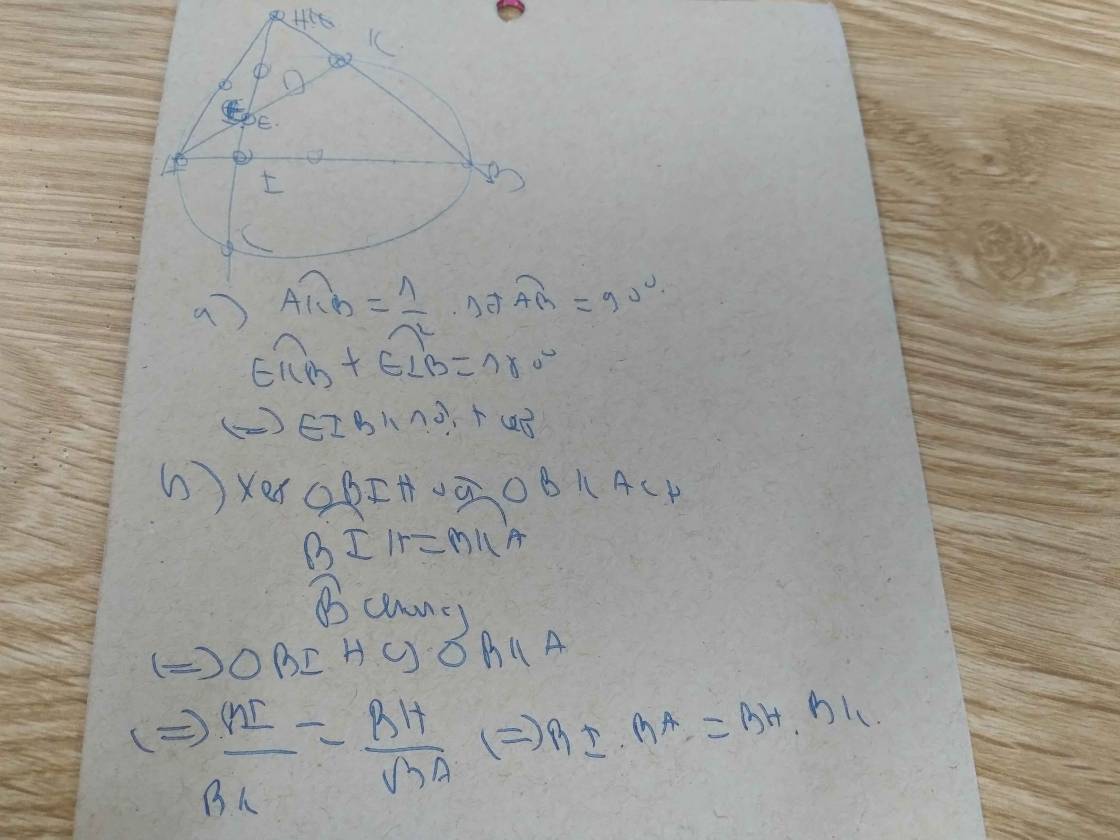Cho đường tròn tâm O, hai dây AB > CD. AB cắt CD tại điểm M nằm ngoài đường tròn (O) (A nằm giữa M và B; C nằm giữa M và D). Gọi H, K lần lượt là trung điểm AB, CD.
Chứng minh MH > MK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C
cauvangbietboi
6 tháng 8 2022
Đúng(0)
Những câu hỏi liên quan
6 tháng 1 2023
a: Xét ΔOBA vuông tại B có BH là đường cao
nên OH*OA=OB^2=R^2
b: Xét ΔABC và ΔADB có
góc ABC=góc ADB
góc BAC chung
Do đó; ΔABCđồng dạng với ΔADB
=>AB/AD=AC/AB
=>AB^2=AD*AC
=>AD*AC=AH*AO
9 tháng 1 2023
a: OH*OM=OA^2=R^2
b: Xét tứ giác MAIO có góc MIO=góc MAO=90 độ
nên MAIO là tứ giác nội tiếp
TY
16 tháng 12 2021
Vì MOH và MOK là tam giác vuông
vậy ta có
MH²+OH²=MK²+OK²
có:AB<CD
⇒OH²<OK²
⇒MH²>MK²⇒MH>MK
CM
11 tháng 1 2018
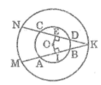
Kẻ OI ⊥ AB, OE ⊥ CD
Trong (O; OA) ta có: AB < CD (gt)
Suy ra : OI > OE (dây lớn hơn gần tâm hơn)
Trong (O ; OK) ta có : OI > OE (cmt)
Suy ra : KM < KN (dây gần tâm hơn thì lớn hơn)
1 tháng 1 2022
b: Xét tứ giác MAIO có
\(\widehat{OIM}=\widehat{OAM}=90^0\)
Do đó: MAIO là tứ giác nội tiếp
7 tháng 12 2022
a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)