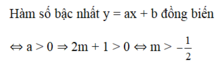Tìm m để hàm số y = (3m-x2)x +2m+3 đồng biến trên R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)

Lời giải:
a. $y=mx-x^2-2x+mx^2+m=x^2(m-1)+x(m-2)+m$
Lấy $x_1,x_2\in R$ sao cho $x_1\neq x_2$
$y(x_1)=x_1^2(m-1)+x_1(m-2)+m$
$y(x_2)=x_2^2(m-1)+x_2(m-2)+m$
Để hàm đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{x_1^2(m-1)+x_1(m-2)+m-[x_2^2(m-1)+x_2(m-2)+m]}{x_1-x_2}>0$
$\Leftrightarrow \frac{(m-1)(x_1^2-x_2^2)+(m-2)(x_1-x_2)}{x_1-x_2}>0$
$\Leftrightarrow (m-1)(x_1+x_2)+(m-2)>0$
Với mọi $x_1,x_2\in\mathbb{R}$ thì không có cơ sở để tìm $m$ sao cho hàm đồng biến.
b.
Xét tương tự câu 1, với $x_1\neq x_2\in \mathbb{R}$ thì hàm đồng biến khi:
$(m^2-3m+2)(x_1+x_2)+(m-1)>0$
Với mọi $x_1, x_2\in\mathbb{R}$ thì điều này xảy ra khi:
$m^2-3m+2=0$ và $m-1>0$
$\Leftrightarrow (m-1)(m-2)=0$ và $m-1>0$
$\Leftrightarrow m=2$

\(y'=3x^2-2\left(m+1\right)x-\left(2m^2-3m+2\right)\)
\(\Delta'=\left(m+1\right)^2+3\left(2m^2-3m+2\right)=7\left(m^2+m+1\right)>0\) ; \(\forall m\)
\(\Rightarrow y'=0\) luôn có 2 nghiệm phân biệt
Bài toán thỏa mãn khi: \(x_1< x_2\le2\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x_1-2\right)\left(x_2-2\right)\ge0\\\dfrac{x_1+x_2}{2}< 2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_1x_2-2\left(x_1+x_2\right)+4\ge0\\x_1+x_2< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-\left(2m^2-3m+2\right)}{3}-\dfrac{4\left(m+1\right)}{3}+4\ge0\\\dfrac{2\left(m+1\right)}{3}< 4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2m^2-m+6\ge0\\m< 5\end{matrix}\right.\) \(\Leftrightarrow-2\le m\le\dfrac{3}{2}\)


Đáp án A
Phương pháp giải:
Dựa vào điều kiện để hàm số đồng biến hoặc nghịch biến trên khoảng xác định
Lời giải:
Ta có
y
=
x
3
-
3
m
x
2
+
3
(
2
m
-
1
)
x
+
1
![]() R
R
Hàm số đồng biến trên R ![]() R
R ![]() R
R
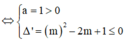
![]()