cho hình bình hành ABCD. Chứng minh rằng: AB2+BC2+CD2+AD2=AC2+BD2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
Ta có: \(AC^2+BD^2=\left(\overrightarrow{AB}+\overrightarrow{AD}\right)^2+\left(\overrightarrow{BC}+\overrightarrow{BA}\right)^2\)
\(=AB^2+AD^2+2\overrightarrow{AB}.\overrightarrow{AD}+BC^2+BA^2+2\overrightarrow{BA}.\overrightarrow{BC}\)
\(=AB^2+AD^2+BC^2+AD^2+2\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{BC}\right)\)
\(=AB^2+AD^2+BC^2+AD^2\)
PT
1
CM
10 tháng 9 2019
Giả sử AB ⊥ CD ta phải chứng minh:
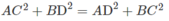
Thật vậy, kẻ BE ⊥ CD tại E, do AB⊥CD ta suy ra CD ⊥ (ABE) nên CD ⊥ AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
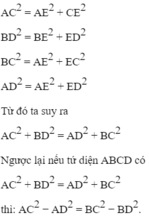
Nếu
A
C
2
−
A
D
2
=
B
C
2
−
B
D
2
=
k
2
thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho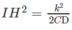 
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD ⊥ AB.
Nếu A C 2 − A D 2 = B C 2 − B D 2 = - k 2 thì ta có và đưa về trường hợp xét như trên A C 2 − A D 2 = B C 2 − B D 2 = - k 2 .
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi A B 2 + C D 2 = A C 2 + B C 2 .
TM
28 tháng 8 2021
- Gọi E là giao điểm của AC và BD
△ABE có trung tuyến BE
\(\Rightarrow BE^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Rightarrow4.BE^2=2\left(AB^2+BC^2\right)-AC^2\)
Mà O là trung điểm BD \(\Rightarrow BD=2.BE\Rightarrow BD^2=4.BE^2\)
\(\Rightarrow BD^2=2\left(AB^2+BC^2\right)-AC^2\)
\(\Rightarrow BD^2+AC^2=2\left(AB^2+BC^2\right)\)
Vậy: \(AC^2+BD^2=2\left(a^2+b^2\right)\left(đpcm\right)\)
(Hình như đây là Toán 10?)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
Kẻ đường cao $BH, DT$ của hình bình hành
Dễ chứng minh $\triangle ADT =\triangle BCH$ (ch-gn)
$\Rightarrow DT=CH; AT=BH$
Áp dụng định lý Pitago:
$AC^2+BD^2=AT^2+TC^2+BH^2+DH^2$
$=(AT^2+BH^2)+TC^2+DH^2)$
$=2AT^2+(DC-DT)^2+(DC+CH)^2$
$=2(AD^2-DT^2)+(DC-DT)^2+(DC-DT)^2$
$=2(b^2-DT^2)+(a-DT)^2+(a+DT)^2$
$=2(b^2+a^2)$
Ta có đpcm.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 7 2023
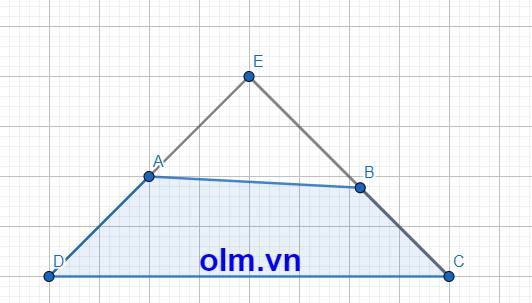
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)
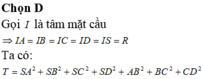
Ta có:
(AB2+BC2+CD2+AD2)-(AC2+BD2)
=(AB2+BC2-AC2)+(AB2+AD2-BD2)
=2*AB*BC*cos(ABC)+2*AB*AD*cos(DAB)
=2*AB*BC*[cos(ABC)+cos(DAB)]=0 (vì 2 góc (ABC) và (DAB) bù nhau)
suy ra đpcm