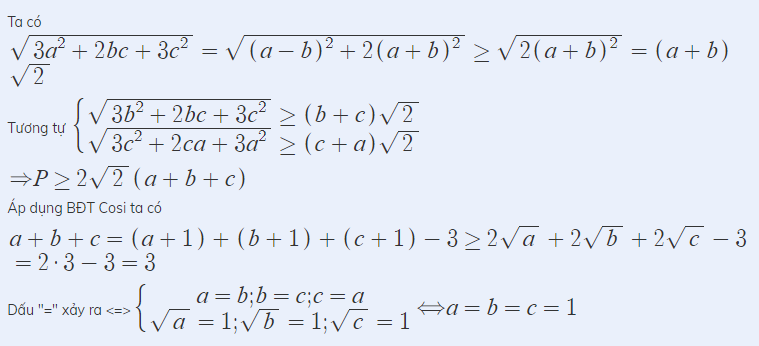Cho a,b,c>0,tim GTNN:\(\frac{\sqrt{a^3c}}{\sqrt{b^3a}+bc}+\frac{\sqrt{b^3a}}{\sqrt{c^3b}+ac}+\frac{\sqrt{c^3b}}{\sqrt{a^3c}+ab}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 6 2020
Chắc là a;b;c dương
Đặt \(\left(a;b;c\right)=\left(\frac{1}{x};\frac{1}{y};\frac{1}{z}\right)\) và vế trái là P
\(P=\frac{x}{\sqrt{z\left(3x+y\right)}}+\frac{y}{\sqrt{x\left(3y+z\right)}}+\frac{z}{\sqrt{y\left(3z+x\right)}}=\frac{x^2}{x\sqrt{3xz+yz}}+\frac{y^2}{y\sqrt{3xy+xz}}+\frac{z^2}{z\sqrt{3yz+xy}}\)
\(P\ge\frac{\left(x+y+z\right)^2}{x\sqrt{3xz+yz}+y\sqrt{3xy+xz}+z\sqrt{3yz+xy}}=\frac{\left(x+y+z\right)^2}{Q}\)
\(Q=\sqrt{x\left(3x^2z+xyz\right)}+\sqrt{y\left(3xy^2+xyz\right)}+\sqrt{z\left(3yz^2+xyz\right)}\)
\(\Rightarrow Q^2\le3\left(x+y+z\right)\left(xy^2+yz^2+zx^2+xyz\right)\)
Không mất tính tổng quát, giả sử \(x=mid\left\{x;y;z\right\}\)
\(\Rightarrow\left(x-y\right)\left(x-z\right)\le0\Rightarrow x^2+yz\le xy+xz\)
\(\Rightarrow zx^2+yz^2\le xyz+xz^2\Rightarrow xy^2+yz^2+zx^2+xyz\le xy^2+2xyz+xz^2\)
\(\Rightarrow xy^2+yz^2+zx^2+xyz\le x\left(y+z\right)^2=\frac{1}{2}.2x\left(y+z\right)\left(y+z\right)\le\frac{4}{27}\left(x+y+z\right)^3\)
\(\Rightarrow Q^2\le3\left(x+y+z\right).\frac{4}{27}\left(x+y+z\right)^3=\frac{4}{9}\left(x+y+z\right)^4\)
\(\Rightarrow Q\le\frac{2}{3}\left(x+y+z\right)^2\)
\(\Rightarrow P\ge\frac{\left(x+y+z\right)^2}{\frac{2}{3}\left(x+y+z\right)^2}=\frac{3}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)
AH
Akai Haruma
Giáo viên
16 tháng 1 2020
Lời giải:
Áp dụng BĐT AM-GM:
\(\sqrt[3]{a+3b}=\sqrt[3]{1.1.(a+3b)}\leq \frac{1+1+a+3b}{3}\)
\(\Rightarrow \frac{1}{\sqrt[3]{a+3b}}\geq \frac{3}{a+3b+2}\)
Hoàn toàn tương tự với các phân thức còn lại và cộng theo vế:
$\Rightarrow P\geq 3\left(\frac{1}{a+3b+2}+\frac{1}{b+3c+2}+\frac{1}{c+3a+2}\right)$
Áp dụng BĐT Cauchy- Schwarz:
\(\frac{1}{a+3b+2}+\frac{1}{b+3c+2}+\frac{1}{c+3a+2}\geq \frac{9}{4(a+b+c)+6}=\frac{9}{4.\frac{3}{4}+6}=1\)
Do đó: $P\geq 3.1=3$
Vậy $P_{\min}=3$ khi $a=b=c=\frac{1}{4}$
D
8 tháng 5 2022
GTNN là tắt của giá trị nhỏ nhất,
Trong bài này bạn biến đổi sao cho biểu thức \(P\ge a\) (số a là số biết trước)
VD: Bạn đưa về dạng nào đó của biểu thức mà nó luôn lớn hơn hoặc bằng \(\dfrac{1}{3}\) Bạn có thể viết \(P\ge\dfrac{1}{3}\) thì GTNN của \(P=\dfrac{1}{3}\) hay \(minP=\dfrac{1}{3}\)
Tìm được GTNN rồi thì bạn tìm ẩn để dấu "=" xảy ra, nghĩa là để BĐT xảy ra dấu =, lúc đó biểu thức P đạt giá trị nhỏ nhất,
VD như: \(minP=\dfrac{1}{3}\) <=> Dấu = xảy ra
<=> x = b (x là ẩn và b là biết trước)
Ở một số bài có thể cho điều kiện của ẩn.