cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\)
chứng minh
a. \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
b. \(\dfrac{a\cdot b}{c\cdot d}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
c.\(\dfrac{2008\cdot a-2009\cdot b}{2009\cdot c+2010\cdot d}=\dfrac{2008\cdot c-2009\cdot d}{2009\cdot a+2010\cdot b}\)

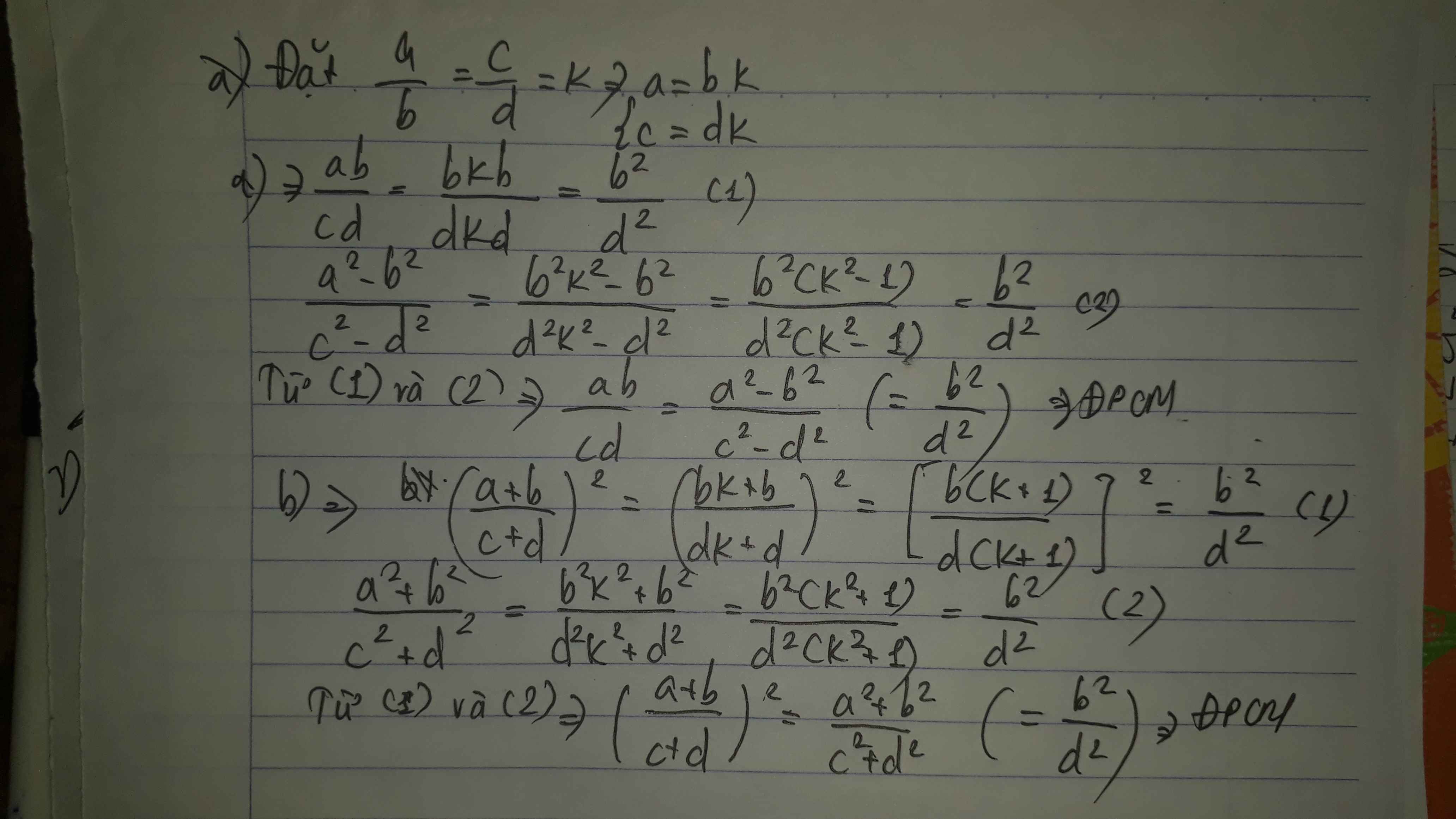
mấy cái đó từ công thức mà ra
a: Đặt a/b=c/d=k
=>a=bk; c=dk
\(\left(\dfrac{a+b}{c+d}\right)^2=\left(\dfrac{bk+b}{dk+d}\right)^2=\dfrac{b^2}{d^2}\)
\(\dfrac{a^2+b^2}{c^2+d^2}=\dfrac{b^2k^2+b^2}{d^2k^2+d^2}=\dfrac{b^2}{d^2}\)
Do đó: \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
b: \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\)
\(\left(\dfrac{a-b}{c-d}\right)^2=\left(\dfrac{bk-b}{dk-d}\right)^2=\dfrac{b^2}{d^2}\)
Do đó: \(\dfrac{ab}{cd}=\left(\dfrac{a-b}{c-d}\right)^2\)