cho tam giác ABC vuông tại A có tia phân giác AD . gọi M,N là hình chiếu của B,C lên đường thẳng AD .
chứng minh rằng : 2AD bé hơn hoặc bằng BM+ CN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

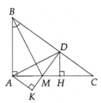
bài 1: cho ΔABC vuông tại B có góc A= 60 độ , vẽ đường phân giác AD (D thuộc BC). Qua D dựng đường thẳng vuông góc với AC tại M và ctaw đường thẳng AB tại N . Gọi I là giao điểm của AD và BM.chứng minh:
a)ΔBAD=ΔMAD
b)AD là đường trung trực của đoạn thẳng BM
c)ΔANC là tam giác đều
d)BI < ND

a) Chú ý tam giác ABD cân tại B nên BM là đường phân giác cũng là đường cao, từ đó B M ⊥ A D .
b) Chú ý AK, BM, DH là ba đường cao của tam giác AMD.

a: góc ABC=2/3*90=60 độ
góc ACB=90-60=30 độ
Xét ΔABD có
AH vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
mà góc B=60 độ
nên ΔABD đều
b: Xét ΔDAC có góc DAC=góc DCA
nên ΔDAC cân tại D
Xét ΔDHA vuông tại H và ΔDGC vuông tại G có
DA=DC
góc HDA=góc GDC
=>ΔDHA=ΔDGC
=>DH=DG và CG=AH
c: ΔBAD cân tại B
mà BM là trung tuyến
nên BM vuông góc AC
Xét ΔDBA có
BM,AH là đường cao
BM cắt AH tại E
=>E là trực tâm
=>DE vuông góc AB
=>DE//AC

a: ΔABC vuông cân tại A có AH là đường cao
nên H là trung điểm của BC
Xét ΔCAB có CH/CB=CM/CA=1/2
nên HM//AB và HM/AB=CH/CB=1/2
=>HM=1/2AB
c: Xét ΔCDB có
CA,BN là đường cao
CA cắt BN tại M
=>M là trực tâm
=>DM vuông góc BC
=>góc MDB=90-45=45 độ
Xét ΔADM vuông tại A có góc ADM=45 độ
nên ΔADM vuông cân tại A
=>AD=AM
