Cho hai điện trở R1 = 5Ω, R2 = 10Ω được mắc song song với nhau.
a) Tính điện trở tương đương của đoạn mạch.
b) Muốn điện trở R'tđ = 3Ω thì phải mắc thêm vào đoạn mạch điện trở bao nhiêu và mắc như thế nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Điện trở tương đương của đoạn mạch:
\(Rtđ=\dfrac{R1.R2}{R1+R2}=\dfrac{15.10}{15+10}=6\left(\Omega\right)\)
b) Cường độ dòng điện chạy qua điện trở
\(I=\dfrac{U}{Rtđ}=\dfrac{18}{6}=3\left(A\right)\)
a)\(R_1//R_2\)\(\Rightarrow R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{15\cdot10}{15+10}=6\Omega\)
b)\(U_1=U_2=U=18V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{18}{15}=1,2A;I_2=\dfrac{U_2}{R_2}=\dfrac{18}{10}=1,8A\)
c)\(R_2ntR_3\Rightarrow R_{23}=R_2+R_3=10+5=15\Omega\)
\(R_1//\left(R_2ntR_3\right)\)\(\Rightarrow R_{tđ}=\dfrac{R_1\cdot R_{23}}{R_1+R_{23}}=\dfrac{15\cdot15}{15+15}=7,5\Omega\)
\(I=\dfrac{U}{R_{tđ}}=\dfrac{18}{7,5}=2,4A\)

a)\(R_1//R_2\)\(\Rightarrow R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{5\cdot10}{5+10}=\dfrac{10}{3}\Omega\)
b)\(U_1=U_2=U=12V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{12}{5}=2,4A\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{12}{10}=1,2A\)
\(I=I_1+I_2=2,4+1,2=3,6A\)
c)Công sản ra của đoạn mạch:
\(A=UIt=12\cdot3,6\cdot10\cdot60=25920J=25,92kJ\)

Gọi điện trở tương đương của đoạn mạch là R t đ
Vì R 1 , R 2 , R 3 mắc song song với nhau nên ta có:
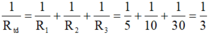
→ R t đ = 3Ω
Chọn B

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{3}{10}\Omega\)
\(\Rightarrow R_{tđ}=\dfrac{10}{3}\Omega\)
\(U_1=U_2=U_3=U=12V\)
\(I=\dfrac{U}{R}=\dfrac{12}{\dfrac{10}{3}}=3,6A\)
\(I_1=I_2=I_3=\dfrac{U_1}{R_1}=\dfrac{12}{10}=1,2A\)
Nếu mắc nối tiếp:
\(R_{tđ}=R_1+R_2+R_3=10+10+10=30\Omega\)

Điện trở tương đương của đoạn mạch là R t đ
Vì R 1 , R 2 , R 3 mắc song song với nhau nên ta có:
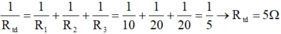

\(R=\dfrac{R1\cdot R2}{R1+R2}=\dfrac{15\cdot10}{15+10}=6\Omega\)
\(U=U1=U2=18V\)
\(\Rightarrow\left\{{}\begin{matrix}I1=U1:R1=18:15=1,2A\\I2=U2:R2=18:10=1,8A\end{matrix}\right.\)
\(R'=\dfrac{R1\cdot\left(R2+R3\right)}{R1+R2+R3}=\dfrac{15\cdot\left(10+5\right)}{15+10+5}=7,5\Omega\)
\(\Rightarrow I'=U:R'=18:7,5=2,4A\)
a)\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{15\cdot10}{15+10}=6\Omega\)
b)\(U_1=U_2=U_m=18V\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{18}{15}=1,2A\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{18}{10}=1,8A\)
c)\(R_1//\left(R_2ntR_3\right)\)
Bạn tự vẽ mạch nhé, mình viết cấu tạo mạch rồi.
\(R_{23}=R_2+R_3=10+5=15\Omega\)
\(R_{tđ}=\dfrac{R_{23}\cdot R_1}{R_{23}+R_1}=\dfrac{15\cdot15}{15+15}=7,5\Omega\)
\(I_m=\dfrac{U_m}{R_{tđ}}=\dfrac{18}{7,5}=2,4A\)
a) Điện trở tương đương của đoạn mạch là:
\(R_{TĐ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{5\cdot10}{5+10}=\dfrac{10}{3}\approx3,33\left(\Omega\right)\)
b) Câu b đề thiếu điện trở đó bao nhiêu ôm
a) Điện trở tương đương của đoạn mạch là:
RTĐ=\(\dfrac{R_1R_2}{R_1+R_2}=\dfrac{5.10}{5+10}=3.33\left(\Omega\right)\)
b) Gọi R3 là điện trở cần phải mắc thêm vào đoạn mạch
vì RTD lúc này trong mạch < R'TD theo đề ở câu b)
=> phải mắc thêm 1 điện trở song song với điện trở R12
ta có:
\(\dfrac{1}{R'_{TD}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}\)
=>\(\dfrac{1}{3}=\dfrac{1}{5}+\dfrac{1}{10}+\dfrac{1}{R_3}\)
Giải phương trình trên:
=>\(\dfrac{1}{R_3}=\dfrac{1}{3}-\dfrac{3}{10}=0,33\left(\Omega\right)\)=> R3=30(Ω)