2. Cho 3 điểm phân biệt A,B,C thẳng hàng và 3 điểm phân biệt B,C,D thẳng hàng. Hai đường thẳng AB & BD có là 2 đường thẳng phân biệt ko . Vì sao ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 9 2017
Hai đường thẳng AC và BD ko phải là hai đường thẳng phân biệt vì hai đường thẳng trên có 1 điểm trùng nhau
HS
28 tháng 9 2019
A) với 2 điểm , ta vẽ dc 1 đường thẳng
B) từ 1 điểm ta nối với 2 điểm còn lại, ta vẽ dc 2 dt. Với 3 điểm như thế, ta vẽ dc 2.3=6 dt(đường thẳng). Mỗi dt như vậy bị lặp lại 2 lần nên số dt ta vẽ dc là 6:2=3dt
C)từ 1 điểm ta nối với 3 điểm còn lại, ta vẽ dc 3 dt. Với 4 điểm như thế, ta vẽ dc 3.4=12 dt(đường thẳng). Mỗi dt như vậy bị lặp lại 2 lần nên số dt ta vẽ dc là 12:2=6 dt
D)từ 1 điểm ta nối với 9 điểm còn lại, ta vẽ dc 9 dt. Với 10 điểm như thế, ta vẽ dc 2.3=6 dt(đường thẳng). Mỗi dt như vậy bị lặp lại 2 lần nên số dt ta vẽ dc là 6:2=3
E)từ 1 điểm ta nối với n điểm còn lại, ta vẽ dc n-1 dt. Với n điểm như thế, ta vẽ dc n.(n-1) dt(đường thẳng). Mỗi dt như vậy bị lặp lại 2 lần nên số dt ta vẽ dc là n.(n-1):2 dt
CM
26 tháng 6 2018
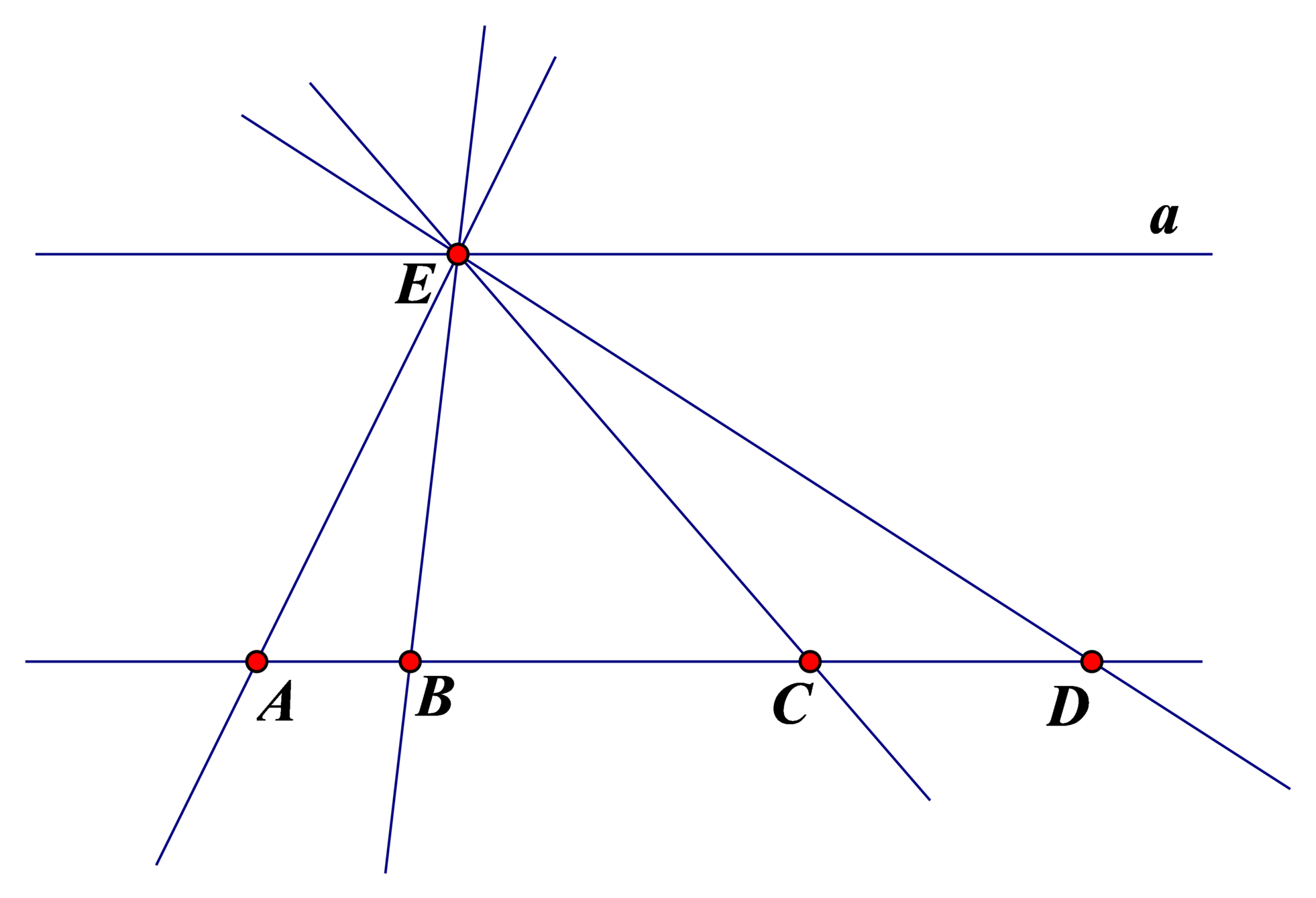
- Có năm đường thảng phân biệt trong hình vẽ, đó là: EA , EB , EC , ED , AB .
- Hai đường thẳng AB và CD trùng nhau; đường thẳng a song song với đường thẳng AB nên cũng song song với đường thẳng CD. Do đó, đường thẳng a không cắt đường thẳng CD.
LH
20 tháng 5 2017
Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau :
a) Với hai điểm (phân biệt) cho trước
Vẽ đc 1
b) Với ba điểm (phân biệt) cho trước và không thẳng hàng
Vẽ đc 3
c) Với bốn điểm (phân biệt) cho trước, trong đó không có 3 điểm nào thẳng hàng
Vẽ đc 6
31 tháng 7 2017
Cho biết có thể vẽ được bao nhiêu đường thẳng (phân biệt) trong mỗi trường hợp sau:
a, Với hai điểm (phân biệt)cho trước: vẽ được 2
b, Với ba điểm (phân biệt) cho trước và không thẳng hàng: vẽ được 3
c,Với bốn điểm phân biệt cho trước trong đó không có 3 điểm nào thẳng hàng: vẽ được 6