Tính x, y biết AB //CD//EF/GH 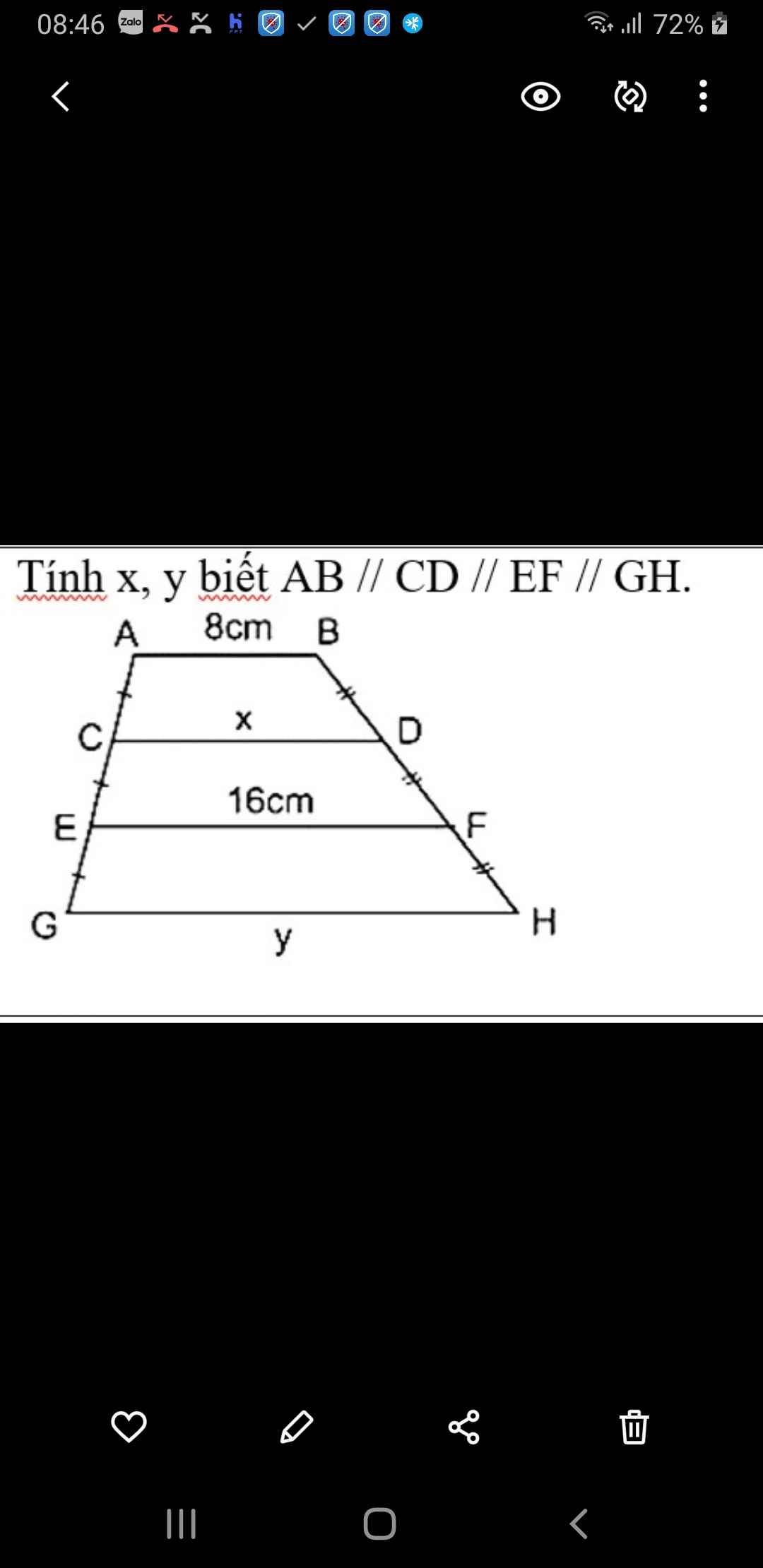
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Hình thang CDHG có: CE = GE , DF = HF ( gt )
=> EF là đường TB của hình thang.
=> EF = \(\dfrac{CD+GH}{2}\) = \(\dfrac{12+16}{2}\) = 14 cm ( hay y = 14 cm )
Hình thang ABFE có: AC = CE, BD = DF ( gt )
=> CD là đường TB của hình thang trên.
=> CD = \(\dfrac{AB+EF}{2}\)
mà CD = 12 cm, EF = 14 cm ( cmt )
=> AB = 12.2 - 14 = 10 cm ( hay x = 10 cm )
Vậy x = 10 cm, y = 14 cm

+ Tính x :
AB // EF nên tứ giác ABFE là hình thang
Hình thang ABFE có: CA = CE và DB = DF
⇒ CD là đường trung bình của hình thang ABFE
⇒ CD = (AB + EF)/2
hay x = (8 + 16)/2 = 12(cm)
+ Tính y:
CD // GH nên tứ giác CDHG là hình thang
Hình thang CDHG có : EC = EG, FD = FH
⇒ EF là đường trung bình của hình thang CDHG
⇒ EF = (CD + GH)/2
hay (x + y)/2 = 16cm ⇒ x + y = 32cm
Mà x = 12cm ⇒ y = 20cm.
Vậy x = 12cm và y = 20cm.

AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE
Do đó : \(CD=\frac{AB+EF}{2}=\frac{8+16}{2}=12\)
hay x = 12
Tương tự CDHG là hình thang , EF là đường trung bình hình thang CDHG
Do đó : \(EF=\frac{CD+GH}{2}\Rightarrow GH=2EF-CD=2.16-12=20\)
hay y = 20
Vaayj x = 12 ; y = 20

\(\dfrac{AB}{CD}=\dfrac{EF}{GH}\)
=>\(\dfrac{AB}{CD}+1=\dfrac{EF}{GH}+1\)
=>\(\dfrac{AB+CD}{CD}=\dfrac{EF+GH}{GH}\)
AB/CD=EF/GH
nên CD/AB=GH/EF
=>\(\dfrac{CD}{AB}+1=\dfrac{GH}{EF}+1\)
=>\(\dfrac{CD+AB}{AB}=\dfrac{GH+EF}{EF}\)
=>\(\dfrac{AB}{CD+AB}=\dfrac{EF}{EF+GH}\)


Chọn từ, cụm từ hoặc kí hiệu : lớn hơn, nhỏ hơn, bằng nhau, có cùng độ dài; <; >; =, điền vào chỗ trống (.....) dưới đây để diễn ta đúng về việc so sánh độ dài đoạn thẳng.
a) AB ...LỚN HƠN ..CD hay CD .NHỎ HƠN...AB hoặc AB ..>...CD hoặc CD ...<....AB
b) CD và GH.....BẰNG NHAU....hoặc CD và GH ....CÓ CÙNG ĐỘ DÀI......hoặc CD ...=.....GH
c) AB ..LỚN HƠN......EF hay EF ....NHỎ HƠN.........AB hoặc AB ..>.......EF hoặc EF ...<.....AB

Bài giải:
AB // EF nên ABFE là hình thang CA = CE và DB = DF nên CD là đường trung bình của hình thang ABFE.
Do đó: CD = \(\dfrac{AB+EF}{2}\) = \(\dfrac{8+16}{2}\) = 12
Hay x = 12
Tương tự CDHG là hình thang, EF là đường trung bình của hình thang CDHG.
Nên EF = \(\dfrac{CD+GH}{2}\) => GH = 2EF -CD = 2.16 - 12
GH = 20 hay y = 20
Vậy x = 12, y = 20
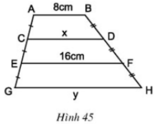
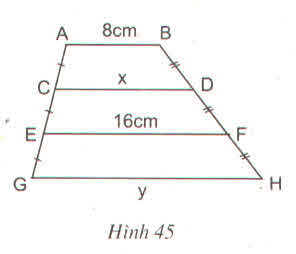
\(AB//EF\) nên \(ABFE\) là hình thang
\(\left\{{}\begin{matrix}AC=CE\\BD=BF\end{matrix}\right.\Rightarrow CD\) là đường trung bình hình thang \(ABFE\)
\(\Rightarrow x=CD=\dfrac{AB+EF}{2}=\dfrac{24}{2}=12\left(cm\right)\)
\(CD//GH\) nên \(CDHG\) là hình thang
\(\left\{{}\begin{matrix}CE=EG\\HF=FD\end{matrix}\right.\Rightarrow EF\) là đường trung bình hình thang \(CDHG\)
\(\Rightarrow EF=16=\dfrac{CD+GH}{2}=\dfrac{12+y}{2}\\ \Rightarrow12+y=32\Rightarrow y=20\left(cm\right)\)