cho các đường thẳng (d1): y=4mx-(m+5) và (d2): y=(3m^2+1)x+(m^2-9)
a)với giá trị nào của m thì d1//d2 b) với giá trị nào của m thì (d1) cắt (d2) tìm tọa độ giao điểm khi m=2 c) chứng minh rằng khi m thay đổi thì đường thẳng (d1) luôn đi qua điểm cố định A; (d2) đi qua điểm cố định B. Tính BA

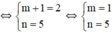
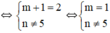
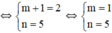
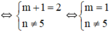
a: Để d1//d2 thì \(\left\{{}\begin{matrix}3m^2+1-4m=0\\-m-5< >m^2-9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(3m-1\right)\left(m-1\right)=0\\m^2-9+m+5< >0\end{matrix}\right.\)
=>m=1/3 hoặc m=1
b: Để hai đường cắt nhau thì (3m-1)(m-1)<>0
hay \(m\notin\left\{\dfrac{1}{3};1\right\}\)