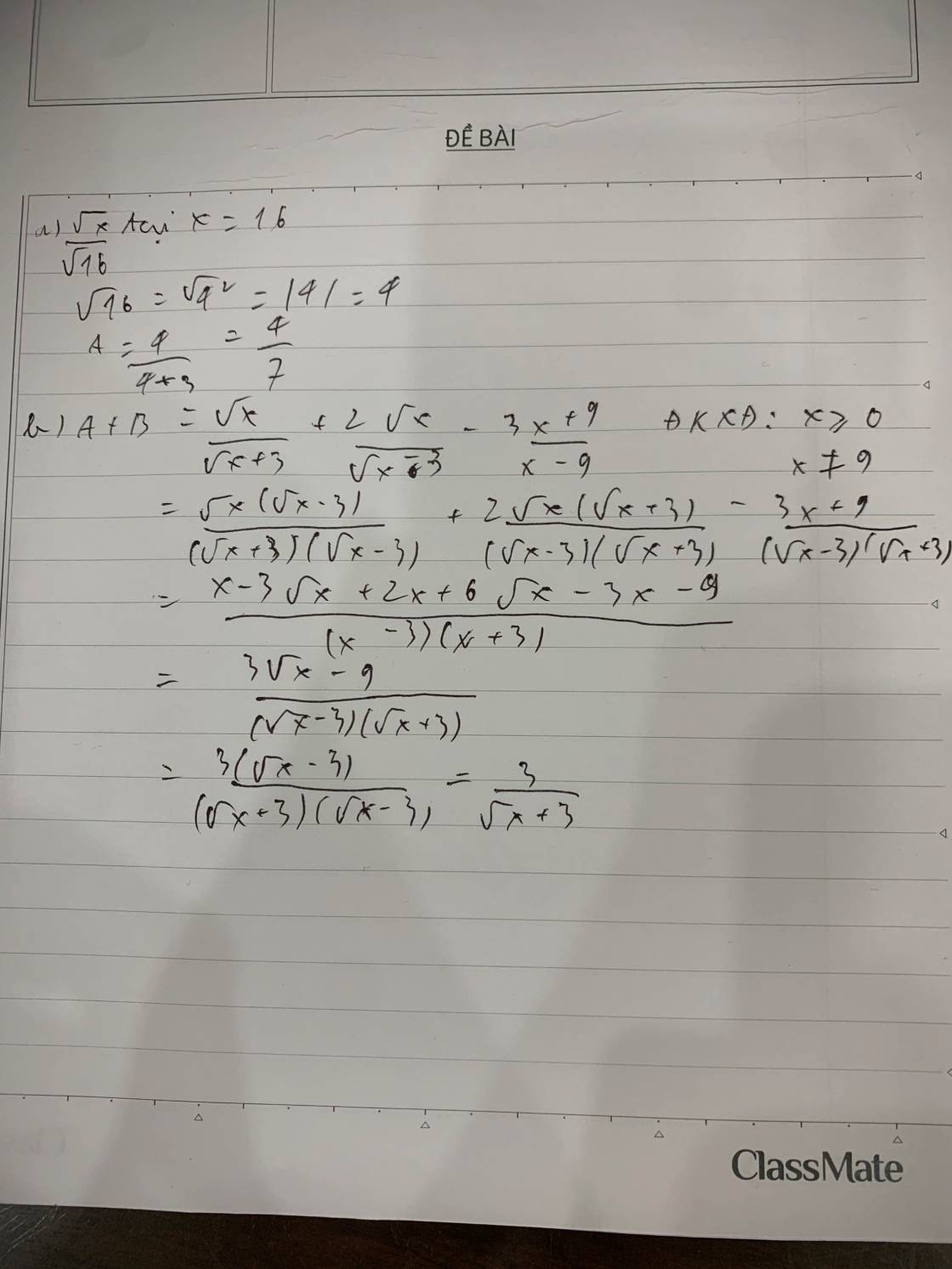Cho x = \(\sqrt{3\sqrt{10}-9}\) . Tính A = (x4 - 4x2 +3)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 7 2021
a) Ta có: \(P=\left(\dfrac{x+3}{x-9}+\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(=\dfrac{x+3+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
b) Ta có: \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=5+\sqrt{2}-4-\sqrt{2}\)
=1
Thay x=1 vào P, ta được:
\(P=\dfrac{1+1}{1+3}=\dfrac{2}{4}=\dfrac{1}{2}\)
31 tháng 8 2021
a: Thay \(x=6-2\sqrt{5}\) vào A, ta được:
\(A=1-\dfrac{\sqrt{5}-1}{\sqrt{5}-1+1}=1-\dfrac{\sqrt{5}-1}{\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)
b: Ta có: P=A:B
\(=\left(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{5\sqrt{x}-10}{x-5\sqrt{x}+6}\right)\)
\(=\dfrac{1}{\sqrt{x}+1}:\dfrac{x-4\sqrt{x}+3-x+4+5\sqrt{x}-10}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{1}{\sqrt{x}+1}:\dfrac{1}{\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
26 tháng 6 2023
Giải
Ta có:
\(x=\sqrt{2+\sqrt{2+\sqrt{3}}-\sqrt{6-3\sqrt{2+\sqrt{3}}}}\)
Khi đó:
\(x^2=\left(\sqrt{2+\sqrt{2+\sqrt{3}}-\sqrt{6-3\sqrt{2+\sqrt{3}}}}\right)^2\\ =2+\sqrt{2+\sqrt{3}}+6-3\sqrt{2+\sqrt{3}}-2\sqrt{\left(2+\sqrt{2+\sqrt{3}}\right)\left(6-3\sqrt{2+\sqrt{3}}\right)}\\ =8-2\sqrt{2+\sqrt{3}}-2\sqrt{12-3\left(2+\sqrt{3}\right)}\\ =8-\sqrt{2}.\sqrt{4+2\sqrt{3}}-2\sqrt{6-3\sqrt{3}}\\ =8-\sqrt{2}.\sqrt{4+2\sqrt{3}}-\sqrt{2}.\sqrt{12-6\sqrt{3}}\\ =8-\sqrt{2}.\left(\sqrt{4+2\sqrt{3}}+\sqrt{12-6\sqrt{3}}\right)\\ =8-\sqrt{2}.\left(\sqrt{\left(\sqrt{3}\right)^2+2\sqrt{3}+1}+\sqrt{9-2.3\sqrt{3}+\left(\sqrt{3}\right)^2}\right)\\ 8-\sqrt{2}.\left(\sqrt{\left(\sqrt{3}+1\right)^2}+\sqrt{\left(3-\sqrt{3}\right)^2}\right)\\ =8-\sqrt{2}.\left(\sqrt{3}+1+3-\sqrt{3}\right)\\ =8-4\sqrt{2}\\ \Rightarrow x^4-16x^2=\left(8-4\sqrt{2}\right)^2-16.\left(8-4\sqrt{2}\right)\\ =96-64\sqrt{2}-128+64\sqrt{2}=-32\)
Vậy \(S=-32\)
19 tháng 7 2021
1: Ta có: \(P=\dfrac{x-\sqrt{x}}{x-9}+\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)
2)
a) Thay \(x=\dfrac{9}{4}\) vào P, ta được:
\(P=\left(\dfrac{3}{2}+2\right):\left(\dfrac{3}{2}+3\right)=\dfrac{7}{2}:\dfrac{11}{2}=\dfrac{7}{11}\)
b) Ta có: \(x=\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)
\(=5+\sqrt{2}-4-\sqrt{2}\)
=1
Thay x=1 vào P, ta được:
\(P=\dfrac{1+2}{1+3}=\dfrac{3}{4}\)
AH
Akai Haruma
Giáo viên
5 tháng 9 2023
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.
HP
7 tháng 8 2021
a, ĐK: \(x\le-1,x\ge3\)
\(pt\Leftrightarrow2\left(x^2-2x-3\right)+\sqrt{x^2-2x-3}-3=0\)
\(\Leftrightarrow\left(2\sqrt{x^2-2x-3}+3\right).\left(\sqrt{x^2-2x-3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2-2x-3}=-\dfrac{3}{2}\left(l\right)\\\sqrt{x^2-2x-3}=1\end{matrix}\right.\)
\(\Leftrightarrow x^2-2x-3=1\)
\(\Leftrightarrow x^2-2x-4=0\)
\(\Leftrightarrow x=1\pm\sqrt{5}\left(tm\right)\)
HP
7 tháng 8 2021
b, ĐK: \(-2\le x\le2\)
Đặt \(\sqrt{2+x}-2\sqrt{2-x}=t\Rightarrow t^2=10-3x-4\sqrt{4-x^2}\)
Khi đó phương trình tương đương:
\(3t-t^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=0\\t=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2+x}-2\sqrt{2-x}=0\\\sqrt{2+x}-2\sqrt{2-x}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2+x=8-4x\\2+x=17-4x+12\sqrt{2-x}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(tm\right)\\5x-15=12\sqrt{2-x}\left(1\right)\end{matrix}\right.\)
Vì \(-2\le x\le2\Rightarrow5x-15< 0\Rightarrow\left(1\right)\) vô nghiệm
Vậy phương trình đã cho có nghiệm \(x=\dfrac{6}{5}\)
9 tháng 5 2022
1, Thay x = 16 vào ta được \(A=\dfrac{4}{4+3}=\dfrac{4}{7}\)
2, \(A+B=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{-x+6\sqrt{x}-9}{x-9}=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}-3}{\sqrt{x}+3}=\dfrac{3}{\sqrt{x}+3}\)
Ta có đpcm
29 tháng 7 2021
a) Ta có: \(A=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{3-\sqrt{x}}-\dfrac{3x+3}{x-9}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}+1}\)
\(=\dfrac{-3}{\sqrt{x}+3}\)
b) Ta có: \(x=\sqrt{3+2\sqrt{2}}-\sqrt{3-2\sqrt{2}}\)
\(=\sqrt{2}+1-\sqrt{2}+1\)
=2
Thay x=2 vào A, ta được:
\(A=\dfrac{-3}{3+\sqrt{2}}=\dfrac{-9+3\sqrt{2}}{7}\)
16 tháng 9 2021
a: Ta có: \(A=\left(\dfrac{3x+3}{x-9}-\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
\(=\dfrac{3x+3-2x+6\sqrt{x}-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{2\sqrt{x}-2-\sqrt{x}+3}\)
\(=\dfrac{3}{\sqrt{x}+3}\)