cho góc nhọn x bt tgx=3 tính 0
B=cos2(36o)+cos2(54o)- cos2(61o)-cos2(29o)/sin2(24o)+sin2(66o)+sin2(25o)+sin2(650) + 3cotg(67o) / 2tg(23o)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 2 2019
\(\dfrac{1+cos2a-sin2a}{1+cos2a+sin2a}=\dfrac{2cos^2a-2sina.cosa}{2cos^2a+2sinacosa}\)
\(=\dfrac{2cosa\left(cosa-sina\right)}{2cosa\left(cosa+sina\right)}=\dfrac{cosa-sina}{cosa+sina}=\dfrac{\sqrt{2}sin\left(\dfrac{\pi}{4}-a\right)}{\sqrt{2}cos\left(\dfrac{\pi}{4}-a\right)}=tan\left(\dfrac{\pi}{4}-a\right)\)
\(\dfrac{1+cos2a-cosa}{sin2a-sina}=\dfrac{2cos^2a-cosa}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)
2 tháng 11 2021
\(a,A=\left(\cos^220^0+\cos^270^0\right)+\left(\cos^240^0+\cos^250^0\right)\\ A=\left(\cos^220^0+\sin^220^0\right)+\left(\cos^240^0+\sin^240^0\right)=1+1=2\\ b,B=\left(\cos^2\alpha\right)^3+\left(\sin^2\alpha\right)^3+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)\\ B=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
23 tháng 8 2021
\(\cot\alpha=\dfrac{1}{2}\)
\(\sin\alpha=\dfrac{kề}{\sqrt{5}kề}=\dfrac{\sqrt{5}}{5}\)
\(\cos\alpha=\sqrt{1-\dfrac{5}{25}}=\dfrac{2\sqrt{5}}{5}\)
PT
1
CM
26 tháng 8 2019
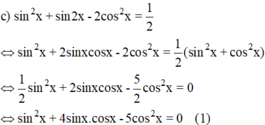
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
(1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0, chia cả hai vế cho cos2x ta được:
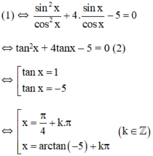
Vậy phương trình có tập nghiệm
(k ∈ Z)
NM
1
15 tháng 7 2023
\(cos^2\left(a-b\right)-sin^2\left(a+b\right)\)
\(=\left(cosa.cosb+sina.sinb\right)^2-\left(sina.cosb+cosa.sinb\right)^2\)
\(=cos^2a.cos^2b+sin^2a.sin^2b-sin^2a.cos^2b-cos^2a.sin^2b\)
\(=cos^2b\left(cos^2a-sin^2a\right)-sin^2b\left(cos^2a-sin^2a\right)\)
\(=\left(cos^2b-sin^2b\right)\left(cos^2a-sin^2a\right)\)
\(=cos2a.cos2b\left(dpcm\right)\)
14 tháng 10 2023
Sửa lại đề bài là \(cos\left(15^o+2\alpha\right)\) (chứ không phải là \(cos^2\left(15^o+2\alpha\right)\) nhé)
Ta có \(VT=sin^2\left(45^o+\alpha\right)-sin^2\left(30^o-\alpha\right)-sin15^o.cos^2\left(15^o+2\alpha\right)\)
\(=\left[sin\left(45^o+\alpha\right)+sin\left(30^o-\alpha\right)\right]\left[sin\left(45^o+\alpha\right)-sin\left(30^o-\alpha\right)\right]-sin15^ocos^2\left(15^o+2\alpha\right)\)
\(=2sin\left(\dfrac{75^o}{2}\right)cos\left(\dfrac{2\alpha+15^o}{2}\right).2cos\left(\dfrac{75^o}{2}\right)sin\left(\dfrac{2\alpha+15^o}{2}\right)-sin15^ocos^2\left(15^o+2\alpha\right)\)
\(=sin75^o.sin\left(2\alpha+15^o\right)-sin15^o.cos^2\left(2\alpha+15^o\right)\)
\(=sin\left(2\alpha+15^o-15^o\right)\) (dùng \(sin\left(\alpha-\beta\right)=sin\alpha.cos\beta-sin\beta.cos\alpha\))
\(=sin2\alpha=VP\)
Vậy đẳng thức được chứng minh.
14 tháng 10 2023
Mấy chỗ kia bạn sửa hết \(cos^2\left(15^o+2\alpha\right)\) thành \(cos\left(15^o+2\alpha\right)\) nhé.
NC
1
S
8 tháng 8 2021
a) sin230 độ - sin240 độ - sin250 độ + sin2 60 độ
= cos260o - cos250o - sin250o + sin260o
= (cos260o + sin260o) - (cos250o + sin250o)
= 1 - 1 = 0
b) cos225 độ - cos235độ + cos245 độ -cos2 55 độ + cos2 65 độ
= sin265o - sin255o + cos245o - cos255o + cos265o
= (sin265o + cos265o) - (sin255o + cos255o) + cos245o
= 1 - 1 +1/2
= 1/2