Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
nên HK//DE
hay HK//BC
c: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HBD}=\widehat{KCE}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
=>\(\widehat{OCB}=\widehat{OBC}\)
=>ΔOBC cân tại O
=>OB=OC
mà HB=CK
nên OB+HB=OC+CK
=>OH=OK
hay ΔOHK cân tại O
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(Hai góc ở đáy của ΔBAC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE(gt)
\(\widehat{HDB}=\widehat{KEC}\)(ΔADB=ΔAEC)
Do đó: ΔHBD=ΔKCE(cạnh huyền-góc nhọn)
c) Ta có: ΔHBD=ΔKCE(cmt)
nên \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
=>ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>AH=AK
Xét ΔADE có AH/AD=AK/AE
nên HK//DE
c:
góc HBD+góc D=90 độ
góc KCE+góc E=90 độ
mà góc D=góc E
nên góc HBD=góc KCE
góc MBC=góc HBD
góc MCB=góc KCE
mà góc HBD=góc KCE
nên góc MBC=góc MCB
=>ΔMBC cân tại M
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
SUy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HDB}=\widehat{KEC}\)
Do đó: ΔHBD=ΔKCE
Suy rA: \(\widehat{HBD}=\widehat{KCE}\)
mà \(\widehat{OBC}=\widehat{HBD}\)
và \(\widehat{OCB}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
c: Xét ΔABO và ΔACO có
AB=AC
BO=CO
AO chung
DO đó: ΔABO=ΔACO
Suy ra: \(\widehat{BOA}=\widehat{COA}\)
hay OA là tia phân giác của góc BOC
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Dođó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
Do đó: HK//DE
hay HK//BC
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
a) Tam giác ABC cân tại A (gt) \(\Rightarrow\widehat{ABC}=\widehat{ACB}\) (Tính chất tam giác cân).
Mà \(\left\{{}\begin{matrix}\widehat{ABC}+\widehat{ABD}=180^o.\\\widehat{ACB}+\widehat{ACE}=180^o.\end{matrix}\right.\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}.\)
Xét tam giác ABD và tam giác ACE:
+ AB = AC (Tam giác ABC cân tại A).
+ \(\widehat{ABD}=\widehat{ACE}\left(cmt\right).\)
+ BD = CE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác ACE (c - g - c).
\(\Rightarrow\) AD = AE (Cặp cạnh tương ứng).
\(\Rightarrow\) Tam giác ADE cân tại A (đpcm).
b) Tam giác ADE cân tại A (cmt). \(\Rightarrow\widehat{ADE}=\widehat{AED}\) (Tính chất tam giác cân).
Xét tam giác DHB và tam giác EKC (\(\widehat{DHB}=\widehat{EKC}=90^o\)) :
+ \(\widehat{HDB}=\widehat{KEC}\) (\(\widehat{ADE}=\widehat{AED}\)).
+ BD = CE (gt).
\(\Rightarrow\) Tam giác DHB = Tam giác EKC (cạnh huyền - góc nhọn).
\(\Rightarrow\) BH = CK (Cặp cạnh tương ứng).
Ta có: \(\left\{{}\begin{matrix}AH+HD=AD.\\AK+KE=AE.\end{matrix}\right.\)
Mà HD = KE (Tam giác DHB = Tam giác EKC); AD = AE (cmt).
\(\Rightarrow\) AH = AK \(\Rightarrow\) Tam giác AHK cân tại A. \(\Rightarrow\) \(\widehat{AHK}=\left(180^o-\widehat{A}\right):2.\)
Mà \(\widehat{ADE}=\left(180^o-\widehat{A}\right):2\) (Tam giác ADE cân tại A).
\(\Rightarrow\) \(\widehat{AHK}=\widehat{ADE}.\)
Mà 2 góc này ở vị trí đồng vị.
\(\Rightarrow\) HK // BC (dhnb).
c) Tam giác DHB = Tam giác EKC (cmt). \(\Rightarrow\) \(\widehat{HBD}=\widehat{KCE}\) (2 góc tương ứng).
Mà \(\widehat{HBD}=\widehat{CBO}\); \(\widehat{KCE}=\widehat{BCO}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{BCO}=\widehat{CBO}\). \(\Rightarrow\) Tam giác OBC là tam giác cân tại O.
d) Xét tam giác ABC cân tại A có: AM là trung tuyến (M là trung điểm BC).
\(\Rightarrow\) AM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) \(AM\perp BC.\) (1)
Xét tam giác OBC cân tại O: OM là trung tuyến (M là trung điểm BC).
\(\Rightarrow\) OM là đường cao (Tính chất các đường trong tam giác cân).
\(\Rightarrow\) \(OM\perp BC.\) (2)
Từ (1) và (2) \(\Rightarrow\) 3 điểm O; A; M thẳng hàng.
\(\Rightarrow\) \(M\in AO.\)
Mà O là giao điểm của BH; CK (gt).
\(\Rightarrow\) O là giao điểm của AM; BH; CK.
\(\Rightarrow\) AM; BH; CK đồng quy (đpcm).
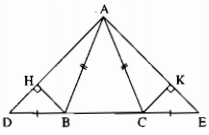
a) Vì tg ABC cân=> ^ABC = ^ACB mà 180-ABC=ABD và 180-ACB=ACE
=> ^ABD = ^ACE
TG ABD = TG ACE (c.g.c)
=> ABD=ACE => TG ADE cân(đpcm)
b) * CM được TG HBD = TG KCE (cạnh huyền- góc nhọn)
=> BH=CK (đpcm)
=> DH=KE
* Ta có: AD = AE (vì TG ADE cân)
DH=KE(CMT)
mà AD - DH = AH
AE - KE = AK
=> AH = AK
và DH=KE ( CMT)
Do đó: HK là đường trung bình của TG ADE
=> HK // DE
c, ý b là BOC?
^HBD=^KCE (TG HBD= TG KCE )
=> ^CBO = ^BCO (đối đỉnh vs 2 góc = nhau)
=> TG OBC cân
*